A triangle's vertices are three independent uniformly random points in the interior of a right cone with base radius $1$ and height $h$.
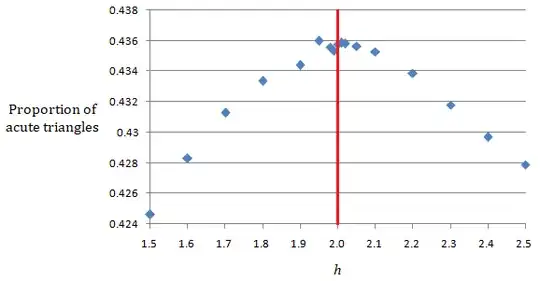
For various values of $h$, I simulated $10^6$ random triangles, and recorded the proportion of triangles that are acute.
Is the following conjecture true: The probability that the triangle is acute, is maximized when $h=2$ (that is, when the cone's height and base diameter are equal).
(For comparison, it is known that if a triangle's vertices are three independent uniformly random points in the interior of a sphere, then the probability that the triangle is acute is $\frac{33}{70}\approx0.471$.)
How I picked random points
Assume the vertex of the cone is $(0,0,0)$ and the rim of the cone is $x^2+y^2=1,z=h$.
The coordinates of the random points in the interior of the cone are:
$$\left(t_1^{1/3}\sqrt{r_1}\cos\theta_1,\space t_1^{1/3}\sqrt{r_1}\sin\theta_1,\space t_1^{1/3}h\right)$$ $$\left(t_2^{1/3}\sqrt{r_2}\cos\theta_2,\space t_2^{1/3}\sqrt{r_2}\sin\theta_2,\space t_2^{1/3}h\right)$$ $$\left(t_3^{1/3}\sqrt{r_3}\cos\theta_3,\space t_3^{1/3}\sqrt{r_3}\sin\theta_3,\space t_3^{1/3}h\right)$$
where the $t$'s and $r$'s are independent uniformly random real numbers between $0$ and $1$, and the $\theta$'s are independent uniformly random real numbers between $0$ and $2\pi$.
(I tested my distribution by generating many random points using my distribution, and recording the proportion that are within a certain sphere that is located completely within the cone. I varied the size and location of the sphere. The proportion is always very close to the ratio of the volume of the sphere to the volume of the cone, as it should be.)
We can assume without loss of generality that $\theta_1=0$, but that still leaves us with many variables.
This question was inspired by another question about random triangles in cones.