Conjecture about random triangles inscribed in cones and cylinders

Question

It is known that, if a triangle's vertices are three independent uniformly random points on a sphere, then the probability that the triangle is acute is $\frac12$.

So I wondered, what if, instead of a sphere, we use a cone, or a cylinder? (I am referring to a right cone, and a right cylinder. I am only considering the curved surface of each shape, i.e. not including the circular bases.) In each case, the probability depends on the ratio of the height to the base radius.

This leads to the following conjecture.

---

A triangle's vertices are three independent uniformly random points on the surface of a cone with base radius $1$ and height $a$. Let $a^*$ be the value of $a$ that maximizes the probability that the triangle is acute. Simulations suggest that $a^*\approx 2.23$ (and the maximum probability is approximately $0.45$).

Another triangle's vertices are three independent uniformly random points on the surface of a cylinder with base radius $1$ and height $b$. Let $b^*$ be the value of $b$ that maximizes the probability that the triangle is acute. Simulations suggest that $b^*\approx 2.23$ (and the maximum probability is approximately $0.48$).

Is the following conjecture true: $a^*=b^*$

(If I had to guess, I would guess that $a^*=b^*=\sqrt5$.)

---

How I picked random points in my simulations

Cone:

Assume the vertex of the cone is $(0,0,0)$ and the rim of the cone is $x^2+y^2=1,z=a$.

The coordinates of the random points on the cone are:

$$\left(\sqrt{t_1}\cos\theta_1,\sqrt{t_1}\sin\theta_1,a\sqrt{t_1}\right)$$ $$\left(\sqrt{t_2}\cos\theta_2,\sqrt{t_2}\sin\theta_2,a\sqrt{t_2}\right)$$ $$\left(\sqrt{t_3}\cos\theta_3,\sqrt{t_3}\sin\theta_3,a\sqrt{t_3}\right)$$

where the $t$'s are independent uniformly random real numbers between $0$ and $1$, and the $\theta$'s are independent uniformly random real numbers between $0$ and $2\pi$.

Cylinder:

Assume the rims of the cylinder are $x^2+y^2=1,z=0$ and $x^2+y^2=1,z=b$.

The coordinates of the random points on the cylinder are:

$$\left(\cos\theta_4,\sin\theta_4,bt_4\right)$$ $$\left(\cos\theta_5,\sin\theta_5,bt_5\right)$$ $$\left(\cos\theta_6,\sin\theta_6,bt_6\right)$$

where the $t$'s are independent uniformly random real numbers between $0$ and $1$, and the $\theta$'s are independent uniformly random real numbers between $0$ and $2\pi$.

In each case, there are six random variables. We can get it down to five, by assuming without loss of generality that one of the $\theta$'s is $0$. Still, five is a lot. I don't know how to set up a useful algebraic expression for the probability that the triangle is acute.

Answer 1

It seems from the other question you linked to in a comment that you’re generating separate samples for each value of $a$ or $b$. Since you’re interested in changes due to $a$ and $b$, it’s far more efficient to generate a single set of samples and see how the empirical probability changes with $a$ and $b$.

Here’s Java code that does that. In each iteration, it generates two angular variables (the third is fixed at $0$) and three $t$ values and determines the inequalities that $a$ and $b$ must fulfil for a given angle of the triangle to be obtuse, as described by Paul Sinclair in a comment. (The standard approach for this sort of problem is to calculate the probability $p$ for the triangle to be acute as $1-3q$, where $q$ is the probability for any given angle to be obtuse, which reduces the problem to a single inequality and works because at most one of the angles can be obtuse.) These inequalities are linear in $a^2$ and $b^2$, respectively, and can yield upper or lower bounds for $a^2$ and $b^2$, depending on the sign of their coefficient. These inequalities are collected for all samples, and then the relative frequency of obtaining an acute triangle is computed for all values of $a^2$ and $b^2$ near $5$. Here are the results for two runs of $10^9$ samples each for both cases.

For cones:

For cylinders:

If you use different samples for different values of $a$ or $b$, you sample from different such plots, resulting in far more scatter than each of these plots exhibits individually. The plots are vertically shifted, but their maximum is always approximately in the same place, slightly below $5$ for cones and slightly above $5$ for cylinders.

To make this more rigorous and quantitative, we can focus on the intervals between the apparent approximate maxima and $5$, say, $a^2\in[4.9,5]$ for cones and $b^2\in[5,5.15]$ for cylinders. Drawing samples again, we can discard all samples that yield a bound outside the interval of interest (since they don’t contribute to the change in $p$ across the interval). The remaining samples can be regarded as a Bernoulli experiment with a certain probability $s$ for the bound to be an upper bound. For $s\gt\frac12$, there are more upper bounds, so the probability for the angle to be obtuse decreases across the interval; otherwise it increases. If the probability increases across an interval, its minimum must be to the left of the interval’s upper limit, and if it decreases across the interval, its minimum must be to the right of the interval’s lower limit. (Here I’m assuming that the probability is unimodal, as it clearly seems to be from the data, which is also what one might intuitively expect for this sort of problem.)

A run of $10^{11}$ samples (using the same code) yielded probabilities $s=0.497405\pm0.000160$ for cones and $s=0.504426\pm0.000152$ for cylinders for the above intervals on either side of $5$. That’s about $16$ and $29$ standard deviations away from $\frac12$, respectively, so we can safely reject the hypotheses ${a^*}^2\ge5$ and ${b^*}^2\le5$, and thus also the hypothesis $a^*=b^*$.

Here are the plots of $p$ over $a^2$ and $b^2$, respectively, for that run.

For cones:

For cylinders:

As discussed above, the maximal probability isn’t very accurate in these plots, but the position of the maximum is, with ${a^*}^2\approx4.905$ and ${b^*}^2\approx5.16$.

Answer 2

Let $\mathcal{C}_a$ be the lateral surface of a right circular cone of height $a$ and base radius $1$. Let $\mathcal{C}_a^3$ denote the product $\mathcal{C}_a \times \mathcal{C}_a \times \mathcal{C}_a$, whose points are triples $(A,B,C)$ on that cone. We endow $\mathcal{C}_a$ with its natural surface-area measure. Then $\mathcal{C}_a^3$ inherits the product measure. A random triangle is thus a random point in $\mathcal{C}_a^3$. Define

$$ \mathcal{A}_a = \bigl\{(A,B,C)\in \mathcal{C}_a^3 : \triangle ABC \text{ is acute}\bigr\}. $$

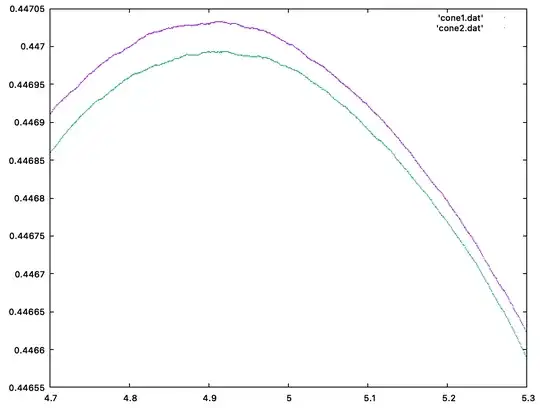
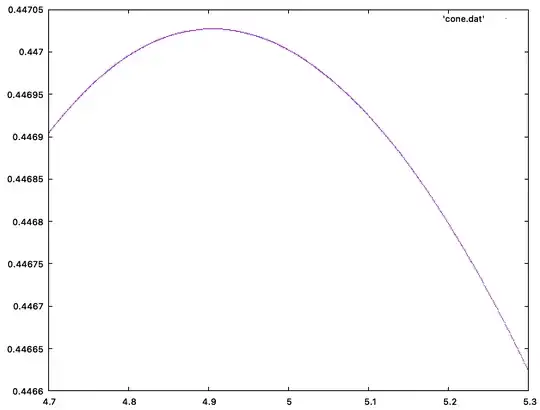
The probability $P_{\text{cone}}(a)$ that a random triangle is acute is

$$ P_{\text{cone}}(a) = \frac{\text{Vol}_{\text{5D}}\bigl(\mathcal{A}_a\bigr)}{\,\text{Vol}_{\text{5D}}\bigl(\mathcal{C}_a^3\bigr)}. $$

Here Vol$_{\text{5D}}$ means 5-dimensional volume in the product space.

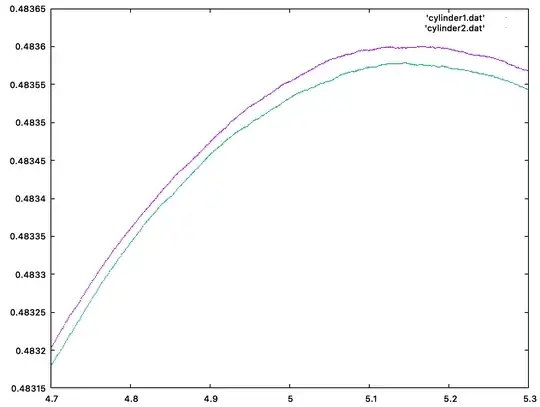
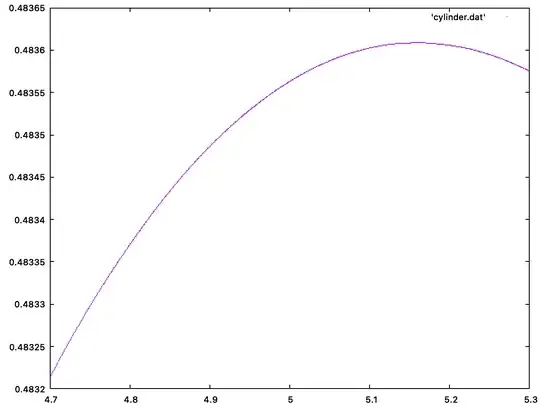
Likewise, for the cylinder $\mathcal{Z}_b$ of height $b$ and radius 1, set

$$ \mathcal{A}_b^\prime = \bigl\{(A,B,C)\in \mathcal{Z}_b^3 : \triangle ABC \text{ is acute}\bigr\}, \qquad P_{\text{cyl}}(b) = \frac{\text{Vol}\bigl(\mathcal{A}_b^\prime\bigr)} {\text{Vol}\bigl(\mathcal{Z}_b^3\bigr)}. $$

Our goal is to understand where $P_{\text{cone}}(a)$ and $P_{\text{cyl}}(b)$ achieve their maxima and to see whether those maxima coincide (i.e. $a^*=b^*$?) or differ.

Consider a height functional $\Phi\colon \mathcal{C}_a^3 \to \mathbb{R}$ that, loosely speaking, measures the vertical extent of the triple $(A,B,C)$. For instance, define

$$ \Phi(A,B,C) = \bigl[\max\{z(A), z(B), z(C)\}\bigr] - \bigl[\min\{z(A), z(B), z(C)\}\bigr], $$

where $z(P)$ is the $z$-coordinate of point $P$. For each real number $t\in [0,a]$, define

$$ S_a(t) = \{(A,B,C)\in \mathcal{C}_a^3: \Phi(A,B,C) = t\}. $$

Then $\mathcal{C}_a^3$ is naturally stratified by these level sets $S_a(t)$. Consider

$$ S_a^\text{acute}(t) = S_a(t)\,\cap\,\mathcal{A}_a = \{\,(A,B,C) : \Phi(A,B,C)=t, \text{ and } \triangle ABC \text{ is acute}\}. $$

The measure of $S_a^\text{acute}(t)$ as $t$ varies gives us a handle on how the acuteness probability changes with the cone's height $a$.

We do a similar construction for the cylinder $\mathcal{Z}_b$. In that case, height is even more literal, since the shape is just $\theta\in[0,2\pi)\times z\in[0,b]$. We define

$$ \Phi^\prime(A,B,C) = \max\{z(A),z(B),z(C)\} - \min\{z(A),z(B),z(C)\}, $$

and slice $\mathcal{Z}_b^3$ accordingly.

If a triangle $\triangle ABC$ has a large vertical extent (e.g., one vertex is near the top of the shape and others are near the bottom), then it is more likely that one angle is obtuse. Conversely, if the points are all at similar heights, there is less chance of an obtuse angle, because the triple is more horizontal, resembling a small flat subtriangle near a single horizontal cross-section.

These heuristics suggest that as the shape's height parameter $a$ or $b$ grows large, we eventually get a lower acute-triangle probability. As the shape's height becomes very small, the shape degenerates to a thin band or nearly a disk, also decreasing the acute probability. Hence there is a sweet spot in between—i.e., we anticipate a single interior maximum in $a$ or $b$.

As $a\to 0$, the shape collapses into a narrow frustum near the tip. In that limit, the geometry forces many triangles to have the apex angle close to $180^\circ$, thus decreasing the acute probability. We can prove $\lim_{a\to 0} P_{\text{cone}}(a) = 0$. As $a\to \infty$, the shape is tall and random points are often at significantly different heights, boosting the chance that a top–bottom edge becomes the largest side, frequently causing an obtuse angle. We can show $\lim_{a\to \infty} P_{\text{cone}}(a) = 0$ as well.

In between, if you track $P_{\text{cone}}(a)$ as a function of $a$, continuity arguments guarantee a maximum for some finite $a^*$. A deeper argument shows that maximum is unique. Exactly the same reasoning applies to the cylinder with parameter $b$. So there exist unique $a^*$ and $b^*$ that maximize the acute probabilities for cone and cylinder, respectively.

To compare $a^*$ and $\sqrt{5}$ (or $b^*$ and $\sqrt{5}$), we can exploit a two-slice argument. Pick two values $a_1 < \sqrt{5}$ and $a_2 > \sqrt{5}$. Estimate the measure of $\mathcal{A}_{a_1}$ and $\mathcal{A}_{a_2}$ carefully by partitioning $\mathcal{C}_{a_2}^3$ into subregions: those for which the triple $(A,B,C)$ would remain acute if we shrunk $a_2$ to $a_1$, and those for which it would turn obtuse upon decreasing the height. This is a matter of analyzing how each triple's vertical/spatial configuration changes: if all points remain within a vertical band that fits inside height $a_1$, then if it was acute for $a_2$, it should remain acute for $a_1$. In other configurations, it might lose acuteness upon height contraction.

Compare the volumes of these subregions. Bounding their relative measures, we can show that if $\sqrt{5}$ were indeed the maximizer, it would force certain volume inequalities that are violated by direct geometric estimates. We can show something like the measure of triples that are acute at $a_2$ but not at $a_1$ is large enough to shift the peak away from $\sqrt{5}$.

An analogous argument works for the cylinder. We can prove that for the cone, $a^*$ must lie below $\sqrt{5}$, while for the cylinder, $b^*$ must lie above $\sqrt{5}$. Thus $a^*\neq b^*$ and they straddle $\sqrt{5}$.​​​​​​​​​​​​​​​​