As i saw the question, i tried to find first a natural geometric proof of problem Q3 in the Olympiad competition, as linked by OP. Now i have one, and although this answer does not have in its main focus the simplification of the given fraction involving trigonometric expression, it may be useful (for the community) so see how the present question emerged from Q3, and how to attack it seeing through the geometric prism. There will be four parts, $\bf(A)$ a natural geometric approach of Q3, $\bf(B)$ how does the OP fraction appear from Q3, and why we want it as $\tan x$ for an explicit angle $x$, $\bf(C)$ a simplification of this fraction (and this part addresses explicitly the question), and $\bf(D)$ an alternative way to attack the Olympiad problem Q3 by trigonometric means.
$\bf(A)$ Yes, i agree, randomly searching for auxiliary points, lines, and circles that solve the problem Q3 in a synthetic manner (three new points and nine new lines is too much!) is risky in the condition of an Olympiad. Trigonometry would be also my weapon of choice. But there is one natural idea! Try to realize the given constellation of points "inside a regular polygon". There is a psychological barrier to do so, when the angles involved are $24^\circ$ and $54^\circ$ with a gcd of $6^\circ$, because this leads to a regular polygon with $180^\circ/6^\circ=30$ sides. (Well, my solutions using regular $n$-gons for similar problems had still a positive echo for $n$ among $3,4,5,6$, but for $n=30$ generally dismissed, although this common multiple covers a lot of regular sub-gons.)
To make it short, here is the realization:
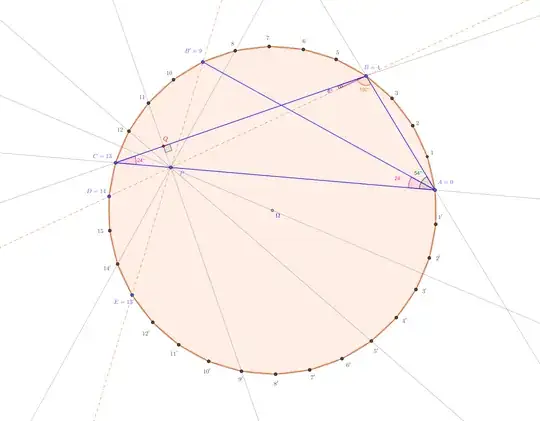
The vertices of the $30$-gon are indexed with elements of the group $\Bbb Z/30$ (integers modulo thirty), and we use as representatives $\pm k$ with $k$ from $0$ to $15$. Instead of $-k$ we also write $k'$. Then the given triangle $\Delta ABC$ is realized with $A=0$, $B=4$, and $C=13$. In order to "copy+paste" the segment $BC$ on the line $AC$, it is natural to build the trapezium $CABB'$ with $B'=9$. The point $P$ from the problem makes $\Delta AB'P$ isosceles in $A$ since $AP=BC=AB’$, where $\angle{PAB’}=24^\circ$, so the angles in $B',P$ are $78^\circ$ each. So $B'P$ passes through the vertex $E:=13'$. We also use the point $D=14$, since the problem suggests that the angle in $B$ in $\Delta BCP$ is a "nice angle", and even a raw picture would make us suppose that $BPD$ is a line.
To solve the problem, it is enough to show:
Proposition: (Seven lines concurrence)
The lines $AC=0,13$, and $BD=4,14$, and $B'E=9,13'$ are concurrent in a point $P$ on the common side bisector $b$ of the segments $12,13$ and $0,5'$. The symmetry center $\Omega$ of the $30$-gon is on this side bisector $b$, so through $P$ also pass the reflections $5',12$, and $9',11$, and $8,14'$.
For this, here is a useful lemma, always needed in such situations (when the trigonometric way is allowed). It is also the technique used invariably in such situations in the "555 geometry solutions book". (Solutions to "Geometry in figures", Akopyan, which contains only the problems.) It is Problem 6.10.24 in this book of Chobanov, Dimitrev, Lichev:
Lemma: Let $ABCDEF$ be a cyclic hexagon. Then $AD$, $BE$, $CF$ intersect in a point, iff $AB\cdot CD\cdot EF=BC\cdot DE\cdot FA$.
Proof of the proposition: For the lines $AC$, $BD$, $B'E$ we consider the hexagon $ABB'CDE$, and applying the lemma, we have to show the first and/or the last of the following equivalent relations:
$$
\begin{aligned}
\underbrace{\sin24^\circ}_{2\sin12^\circ\cos12^\circ}
\sin24^\circ\sin18^\circ &=
\underbrace{\sin30^\circ}_{1/2}\sin 6^\circ
\underbrace{\sin78^\circ}_{\cos 12^\circ} \ ,
\\
4\underbrace{\sin12^\circ}_{2\sin6^\circ\cos6^\circ}
\sin24^\circ\sin18^\circ &=
\sin 6^\circ
\ ,
\\
8\cos6^\circ\sin24^\circ\sin18^\circ &= 1
\ ,
\\
4\Big(\sin(24^\circ+6^\circ)+\sin(24^\circ-6^\circ)\Big)\sin18^\circ &= 1
\ ,
\\
2\sin18^\circ +\underbrace{4\sin^2 18^\circ}_{2(1-\cos 36^\circ)} &= 1\ ,
\\
1 + 2\cos 72^\circ - 2\cos 36^\circ &= 0\ ,
\\
1 + 2\cos 72^\circ + 2\cos 144^\circ &= 0\ ,
\end{aligned}
$$
and the last relation is true, consider the regular pentagon centered in the origin with one vertex in $1$, its center mass is zero, so the sum of projections of the vertices on the $Ox$-axis also vanishes. This shows the first claimed concurrence of $AC,BD,B'E$.
To conclude, we replace one of the lines, $B'E$, by its reflection w.r.t. $b$, which is $8,14'$, and show again the concurrence. (This concludes, since two lines remained, they intersect in the "old" point $P$, which is now on both $B'E$ and its $b$-reflection, so it is on $b$.)
The relation to be shown is:
$$
\sin 24^\circ\cdot
\underbrace{\sin 30^\circ}_{1/2}\cdot
\sin 12^\circ\cdot
=
\sin 24^\circ\cdot
\sin 6^\circ\cdot
\underbrace{\sin 84^\circ}_{\cos6^\circ}
\ ,
$$
which is immediate, the formula for the sine of the double angle.
$\square$
This shows the claimed Proposition, and gives a geometric argument for
$$
\widehat{CBP} =
\widehat{CBD} =
\frac 12\overset{\large\frown}{CD}=6^\circ\ .
$$
Usually, when a "kind" of an argument is needed geometrically, a similar "kind" of argument is needed also algebrically. Below we will forget about this proof, and restart.
$\bf(B)$
How is the problem Q3 related to the posted question?
Denote by $x$ the angle $x=\widehat{CBP}$. Let $T$ denote the OP fraction,
$$
T =
\frac
{\sin 102^\circ \sin 24^\circ - \sin 156^\circ\sin 54^\circ}
{\cos 102^\circ \sin 24^\circ - \cos 156^\circ\sin 54^\circ}
\ .
$$
Let $Q$ be the projection of $P$ on $BC$. (With the notations from (A), we a posteriori know that $Q$ is on the line $11,9'$ the $b$-reflection of $BD$.)
By the sine theorem, the sides of $\Delta ABC$ are proportional to the sines of the opposite angles, so we may and do rescale and assume that:
$$
\begin{aligned}
BC &= \sin 54^\circ=\cos 36^\circ\ ,\\
CA &= \sin 102^\circ=\sin 78^\circ=\cos 12^\circ\ ,\\
AB &= \sin 24^\circ\ ,\qquad\text{ and from here:}\\
PC &= AC-AP=AC-BC= \cos 12^\circ -\cos 36^\circ\ ,\\
PQ &= PC\sin 24^\circ = (\cos 12^\circ -\cos 36^\circ)\sin 24^\circ\ ,\\
BQ &= BC-QC=\underbrace{\cos 36^\circ}_{\text{expand }\cos (12^\circ+24^\circ)} - (\cos 12^\circ -\cos 36^\circ)\cos 24^\circ\ ,\\[2mm]
\text{Numerator of $T$}
&=\sin 102^\circ \sin 24^\circ - \sin 156^\circ\sin 54^\circ\\
&=\sin 78^\circ \sin 24^\circ - \sin 24^\circ\sin 54^\circ=PQ\ ,\\[2mm]
\text{Denominator of $T$}
&=\cos 102^\circ \sin 24^\circ - \cos 156^\circ\sin 54^\circ\\
&=-\sin 12\sin 24^\circ+\cos 24^\circ\cos36^\circ=BQ\ ,\\[2mm]
\tan x &=\frac {PQ}{BQ}=T\ .
\end{aligned}
$$
This explains the OP strategy to solve the Olympiad problem, and shows that
we need an explicit simplification of $T$ in the form of $\tan$ of "something", only this form is useful for obtaining the full one mark for the problem Q3.
An equivalent way would be to use the sine theorem in the form
$\displaystyle\frac{\sin(102^\circ-x)}{AP}=\frac{\sin(156^\circ-x)}{AB}$,
then expand the sines in terms of $\sin x$, $\cos x$, and isolate
the equation for $\tan x$. (The other way is more geometric, and $PQ$ can be "better extracted" for the needs that appear below.)
$\bf(C)$
This part addresses the stated question in the form: "How to simplify the fraction $T$ in five minutes, and which is the reason for the chosen computational path (so that it is not an artificial combination of intermediate relations without natural connection)?"
Because we want to show $T=\tan 6^\circ$, it is important to have product expressions, factors, no addition and subtraction in the numerator and denominator of $T$. At least this is the strategy below.
The answer comes only because of the fact, that this strategy works in a (Galois) structural manner, the one good reason to share the thoughts with the community.
A first progress is done by reworking $BQ$, using the picture from $(A)$, and the triangle $\Delta (B,Q,11)$. Its angle in $B$ is $12$ and
in our rescaling (radius is $1/2$) $|B,11|=\sin42^\circ=\cos 48^\circ$, so we expect $BQ=\cos12^\circ\cos 48^\circ$, and indeed, this follows from
$$
2\,BQ =
\underbrace{2\cos 24^\circ\cos36^\circ}_{=\cos12^\circ+\cos60^\circ}
-
\underbrace{2\sin 12\sin 24^\circ}_{=\cos12^\circ-\cos36^\circ}
=
\underbrace{2\cos12^\circ\cos 48^\circ}_{=\cos36^\circ+\cos60^\circ}\ .
$$
Also, in the formula for $PQ$ we use the final product form in
$$
\cos12^\circ-\cos36^\circ=
\cos(24^\circ-12^\circ)-\cos(24^\circ+12^\circ)=
2\sin12^\circ\sin 24^\circ\ $$
And now we are in position to force factors and factorizations, using only angles of the shape $k\cdot 12^\circ$, $k=1,2,4,8,16,\dots$, and try to get rid of the factors in denominator, all but one that should be $\cos 6^\circ$:
$$
\small
\begin{aligned}
T &=
\frac{PQ}{BQ}
=
\frac
{2\sin12^\circ\sin^2 24^\circ}{\cos12^\circ\cos 48^\circ}
=
\frac
{4\sin^212^\circ\sin^2 24^\circ}{2\sin12^\circ\cos12^\circ\cos 48^\circ}
\\
&=
\frac
{4\sin^212^\circ\sin 24^\circ}{\cos 48^\circ}
=
\frac
{8\sin^212^\circ\sin 24^\circ\sin48^\circ}{2\sin48^\circ\cos 48^\circ}
=
\frac
{16\cos 6^\circ\sin 6^\circ\sin12^\circ\sin 24^\circ\sin48^\circ}{\sin96^\circ}
\\
&=16\sin 6^\circ\sin12^\circ\sin 24^\circ\sin48^\circ
\\
&=\frac{\sin6^\circ}{\cos6^\circ}\ \cdot\
\underbrace{16\sin12^\circ\sin 24^\circ\sin48^\circ \sin 96^\circ}_{=1}
\\
&=\tan 6^\circ\ .
\end{aligned}
$$
In order to conclude, let us show that the underbraced product is indeed one:
Lemma: Consider the following expressions $E,F$:
$$
\begin{aligned}
E &=16\cos12^\circ\cos 24^\circ\cos48^\circ \cos 96^\circ\ ,
&&\text{then: } & E &= -1\ ,\\
F &=16\sin12^\circ\sin 24^\circ\sin48^\circ \sin 96^\circ\ ,
&&\text{then: } & F &= +1\ .
\end{aligned}
$$
We need only the expression for $F$, but OP asks for related or unrelated relations that may be helpful in similar situations.
Proof: Of course, $E\ne 0$, so we get:
$$
\begin{aligned}
E\sin12^\circ
&=
16\cos96^\circ\cos 48^\circ\cos24^\circ \cos 12^\circ\sin12^\circ\\
&=
8\cos96^\circ\cos 48^\circ\cos24^\circ \sin24^\circ\\
&=
4\cos96^\circ\cos 48^\circ\sin48^\circ\\
&=
2\cos96^\circ\sin96^\circ\\
&=
\sin192^\circ\\
&=
-\sin12^\circ\ .
\end{aligned}
$$
For $F$ there is no similar trick, but we can compute:
$$
\begin{aligned}
4\sin12^\circ\sin48^\circ
&=
2\cos36^\circ-2\cos 60^\circ=2\cos36^\circ-1\ ,
\\[2mm]
4\sin24^\circ\sin96^\circ
&=
2\cos72^\circ-2\cos 120^\circ=2\cos72^\circ+1\ ,
\\[2mm]
F&=(4\sin12^\circ\sin48^\circ)(4\sin24^\circ\sin96^\circ)
\\
&=(2\cos36^\circ-1)(2\cos72^\circ+1)
\\
&=4\cos36^\circ\cos72^\circ
+\underbrace{(2\cos36^\circ-2\cos72^\circ-1)}_{=0}
\\
&=2\cos(72^\circ-36^\circ) + 2\cos(72^\circ+36^\circ)
=2\cos36^\circ-2\cos72^\circ
\\
&=1\ .
\end{aligned}
$$
We have used exactly the same regular pentagon mass point projection argument as in $(A)$.
$\square$
Note: An argument from Galois theory for both equalities works as follows.
Let $\zeta=\zeta_{30}=\cos \frac\pi{15}+i\sin \frac\pi{15}$ be this primitive cyclotomic root of unity of order $30$. Consider $u=\zeta+\frac 1{\zeta}=2\cos \frac \pi{15}$ and $v=\zeta-\frac 1{\zeta}=2i\sin \frac \pi{15}$. Up to an algebraic unit of norm one, they are $1\pm \zeta^2$, which are elements of norm $1$ over $\Bbb Q$. To compute "the norm", we build the product of all the Galois conjugates. The sign is extracted from the known signs of the factors. Note that the "Frobenius" map $\Phi$ given by $\zeta\to\Phi\zeta:=\zeta^2$ brings $u,v$ in further conjugates, and using them we arrive at the claimed products $E,F$.
$\bf(D)$
Here is an other trigonometric approach for the same Olympiad problem $Q3$.
Let $x$ be the angle to be computed. We start with a proportion of areas,
$$
\frac
{BC\cdot BP\cdot \sin x}
{BP\cdot BA\cdot \sin (102^\circ -x)}
=
\frac
{\operatorname{Area}(BCP)}
{\operatorname{Area}(BPA)}
=
\frac {CP}{PA}
=
\frac {CP}{BC}
\ ,
$$
which gives:
$$
\small
\begin{aligned}
\frac
{\sin x}
{\sin (102^\circ -x)}
&=
\frac{AB\cdot CP}{BC^2}
=
\frac{\sin24^\circ(\cos 12^\circ- \cos36^\circ)}{\sin^2 54^\circ}
=
\frac{2\sin12^\circ\sin^2 24^\circ}{\cos^2 36^\circ}
\\
&=
\frac{4\sin6^\circ\cos6^\circ\sin^2 24^\circ}{\cos^2 36^\circ}
=
\frac {\sin 6^\circ}{\cos 6^\circ}
\cdot
\underbrace{\left(
\frac{4\cos 6^\circ\sin 24^\circ}{2\cos 36^\circ}
\right)^2}_{=1}
\ ,
\end{aligned}
$$
because of the same pentagon mass center argument,
$$
4\cos 6^\circ\sin 24^\circ
=
2\sin(24^\circ+6^\circ)
+
2\sin(24^\circ-6^\circ)
=
1+
2\sin18^\circ
=
1+
2\cos 72^\circ
=
2\cos 36^\circ\ .
$$
The resulted equation is now rephrased equivalently:
$$
\small
\begin{aligned}
\frac
{\sin x}
{\sin (102^\circ -x)}
&=
\frac {\sin 6^\circ}{\cos 6^\circ}
\\
2\sin x\cos 6^\circ &=2\sin (102^\circ -x)\sin 6^\circ\ ,
\\
\sin(x+6^\circ) + \sin(x-6^\circ)
&=
\cos(96^\circ-x) - \cos(108^\circ-x)
\ ,
\end{aligned}
$$
and observe now that the angles $x-6^\circ$ and $96^\circ-x$ sum up to $90^\circ$, so the corresponding trigonometric function that appear as terms above cancel each other, we obtain then $\sin(x+6^\circ)=-\cos(108^\circ-x)$,
i.e. $\sin(x+6^\circ)=\sin(18^\circ-x)$, which leads to $x=6^\circ$.
$\square$
Above there are three more or less different proofs for $x=6^\circ$, $x$ being the wanted angle in $Q3$. One of them addressed directly the simplification of the given expression $T$, the other two are indirect (regarding the question), and give a geometric, respectively a simpler trigonometric approach.
