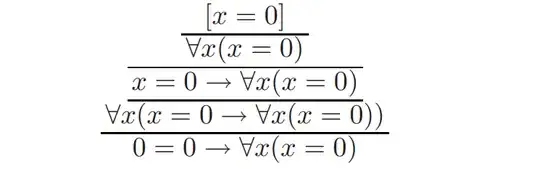-1

The $\forall I$ rule in Val Dalen's Logic and Structure is $\def\f{\varphi}$

$$\frac{\f(x)}{\forall x \f(x)}$$

where $x$ does not appear free on any hypothesis on which $\f(x)$ depends. As an explanation for this restruction, the author shows that if the restriction was removed we could argue as follows:

enter image description here

which is obviously incorrect. As he explains, the $\forall$ introduction at the first step was illegal. What confuses me here is that I thought

$$\vdash \f(x) \ \ \ \ \text{ if and only if } \vdash \forall x \f(x)$$

for any $\f$ with free $x$. I even thought to have proven it. Therefore, the first step in Van Dalen's erroneous proof would be valid, and so would the erroneous argument as a whole.

What am I missing?

The current post is different from this one as I'm presently concerned with the erroneous derivation in the text. In particular, I'm wondering why the first step of the derivation is consistent with the result

$$\vdash \f(x) \ \ \ \ \text{ if and only if } \vdash \forall x \f(x).$$

Sam
  • 5,208
  • 1
    The example above shows that $(x=0) \vdash \forall x (x=0)$ is incorrect. And yes, "if $\vdash (x=0)$, then $\forall x (x=0)$" is correct. The point is: how you can prove $\vdash (x=0)$? in Peano arithmetic? – Mauro ALLEGRANZA Dec 09 '24 at 10:37

1 Answers1

0

What you're missing is the difference between "if $\vdash P$, then $\vdash Q$" and "$P\vdash Q$".

Alex Kruckman
  • 86,811
  • Sorry, but I do not understand. Isn't it also true that $\forall x\phi(x) \vdash \phi(x)$ and $\phi(x)\vdash \forall x\phi(x)$? – Sam Dec 07 '24 at 14:05
  • The first is correct, but the second is wrong. @Sam – Alex Kruckman Dec 07 '24 at 14:32
  • Just think about the meaning: If we assume $\phi$ is true for all $y$, can we conclude $\phi$ is true of $x$? Yes, of course. If we assume $\phi$ is true of $x$, can we conclude $\phi$ is true for all $y$? No, of course not. – Alex Kruckman Dec 07 '24 at 14:35
  • On the other hand, if $\vdash \phi(x)$, this means we can prove $\phi$ is true of $x$ from no assumptions. Since in particular we've made no assumptions on $x$, we should also be able to prove that $\phi$ is true for all $x$, i.e., $\vdash \forall x,\phi(x)$. – Alex Kruckman Dec 07 '24 at 14:43
  • If $\phi(t)$ for some closed term $t$, then naturally we cannot conclude $\forall x\phi(x)$, but my understanding was that $\phi(x)$ for a free $x$ is to be (informally) interpreted as $\forall x\phi(x)$. Put another way, let $T$ be any theory. Do we not have $T\vdash \phi(x) \iff T\vdash \forall x\phi(x)$ with exactly the same proof as in the $\vdash \phi(x) \iff \vdash \forall x\phi(x)$ case? – Sam Dec 07 '24 at 15:13