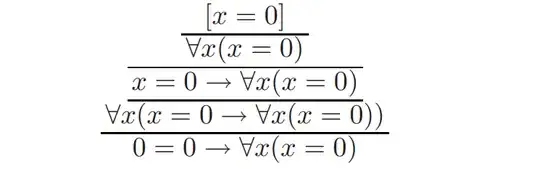On the correct $(\forall)$-introduction rule in Natural Deduction

Question

In a nutshell: is the following the $(\forall)$-introduction rule in Natural Deduction?

$$\frac{\phi[t/x]}{\forall x\phi}\ \ \ \ \ \ \ \ \ \begin{matrix}\text{provided the term $t$ does not occur in $\phi$}\\ \text{nor in any undischarged assumption in the proof of $\phi[t/x]$}\end{matrix} $$

---

I began learning about natural deduction from these notes where the $(\forall)$-introduction rule is written as above except $t$ is a constant, not an arbitrary term. The same happens with $(\exists)$-elimination. Such was one of the reasons I was confused when learning that we are allowed to subsitute general terms when using the rule. From that point on, I have been assuming that the correct $(\forall)$-introduction rule is as written in the notes, but with $t$ standing for an arbitrary term. Realizing I've been assuming this without ever having read the correct rule anywhere explicitly, I thought I should check that my understanding is right.

---

Edit: I asked the following in a separate post which was closed as a duplicate, so I guess I must ask it here:

The $\forall I$ rule in Val Dalen's Logic and Structure is $\def\f{\varphi}$

$$\frac{\f(x)}{\forall x \f(x)}$$

where $x$ does not appear free on any hypothesis on which $\f(x)$ depends. As an explanation for this restruction, the author shows that if the restriction was removed we could argue as follows:

which is obviously incorrect. As he explains, the $\forall$ introduction at the first step was illegal. What confuses me here is that I thought

$$T\vdash \f(x) \ \ \ \ \text{ if and only if } T\vdash \forall x \f(x)$$

for any $\f$ with free $x$. I even thought to have proven it. Therefore, the first step in Van Dalen's erroneous proof would be valid, and so would the erroneous argument as a whole.

What am I missing?

Answer 1

See van Dalen's Logic and Structure (4th ed, 2004), page 91: Instantiation (the Elimination rule) allows for a term whatever.

Intuition: a term is a "name" and if $\varphi$ holds of every objects, we can use every kind of name available in the language: veriables, constants, complex terms.

Generalization (the Intorduction rule) is a little bit tricky; compare van Dalen's form with this one.

The difference is the way to express the proviso needed to avoid the fallacious use of the rule.

In the form $\dfrac { \phi}{\forall x \varphi}$ we have to consider that the premise $\phi$ depends on itself.

In the form "If $\Gamma \vdash \phi[a/x]$, then $ \Gamma \vdash \forall x \phi$" the proviso is that "the parameter (free var) $a$ is required to be “fresh” in the sense of having no occurrences in $\Gamma$".

And see van Dalen, page 93, for the derivation of the second form: "If $\Gamma \vdash \phi(x)$, then $\Gamma \vdash \forall x \phi (x) \text { if } x \notin FV (ψ)$ for all $ψ ∈ Γ$", from the first one.

And page 95: "If [constant] $c$ does not occur in $\Gamma$, then if $\Gamma \vdash \phi (c)$, then $\Gamma \vdash \forall x \phi (x)$".

Also very useful: Dag Prawitz, Natural Deduction. A Proof-Theoretical Study (Almqvist & Wiksell, 1965)

Answer 2

For $\forall$ Introduction, you want $t$ to be a constant ... because with the constraint that that constant should not have been used elsewhere in the proof, we can think of it as an arbitrary object from the domain, and hence the universal generalization is valid. If $t$ was just any variable-free term, things become problematic. Suppose, for example, that you have $P(f(a))$. Now, $a$ may not occur elsewhere in the proof, but we can no longer think of $f(a)$ as an arbitrary object: what if $f$ only covers a subset of the domain? Then we can no longer say that every object has property $P$.

Likewise, for $\exists$ Elimination, you really want to instantiate with a constant, not with any variable-free term. Suppose you have $\exists x \ P(x)$: so some object in the domain has property $P$. But that doesn't mean that $f(a)$ has property $P$ for some object $a$: again, $f$ may not map to the objects that have property $P$.

However, for universal elimination and existential introduction, $t$ can be any variable-free term. For example, if $\forall x \ P(x)$ then clearly we can infer things like $P(f(a))$: $f(a)$ is some object from our domain, and given that all objects from the domain have property $P$, we can infer $P(f(a))$. And if we have $P(f(a))$, then clearly we can infer that there is some object with property $P$, i.e. we can infer $\exists x \ P(x)$.