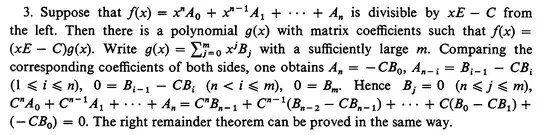1

I am reading "Linear Algebra" by Ichiro Satake.

The following are Exercise 3 and the author's answer to Exercise 3.
I don't understand why the author's answer is long like the following.

My answer is very short:

Let $x^nA_0+x^{n-1}A_1+\cdots+A_n=(xE-C)(x^{n-1}B_0+x^{n-2}B_1+\cdots+B_{n-1})$.

Since $CC^i=C^iC$ for any $i\in\{0,1,2,\dots\}$, $$O=(CE-C)(C^{n-1}B_0+C^{n-2}B_1+\cdots+B_{n-1})\\=C^nB_0+(C^{n-1}B_1-CC^{n-1}B_0)+\cdots+(CB_{n-1}-CCB_{n-2})-CB_{n-1}\\=C^nB_0+(C^{n-1}B_1-C^{n-1}CB_0)+\cdots+(CB_{n-1}-CCB_{n-2})-CB_{n-1}\\=C^nB_0+C^{n-1}(B_1-CB_0)+\cdots+C(B_{n-1}-CB_{n-2})-CB_{n-1}\\=C^nA_0+C^{n-1}A_1+\cdots+A_n.$$

Please compare the above equations with the following equations:

Since $xC^i=C^ix$ for any $i\in\{0,1,2,\dots\}$, $$(xE-C)(x^{n-1}B_0+x^{n-2}B_1+\cdots+B_{n-1})\\=x^nB_0+(x^{n-1}B_1-Cx^{n-1}B_0)+\cdots+(xB_{n-1}-CxB_{n-2})-CB_{n-1}\\=x^nB_0+(x^{n-1}B_1-x^{n-1}CB_0)+\cdots+(xB_{n-1}-xCB_{n-2})-CB_{n-1}\\=x^nB_0+x^{n-1}(B_1-CB_0)+\cdots+x(B_{n-1}-CB_{n-2})-CB_{n-1}\\=x^nA_0+x^{n-1}A_1+\cdots+A_n.$$

Honestly speaking, I think $C^nA_0+C^{n-1}A_1+\cdots+A_n=O$ is an obvious equation.

But I am afraid if my answer is wrong.
Is my answer wrong or bad?

enter image description here

enter image description here

佐武五郎
  • 1,718
  • @user1551 thank you very much for your comment. I edited my question. – 佐武五郎 Aug 17 '24 at 18:14
  • 1
    Your proof is correct, but I don’t agree that the result is obvious. In general, when $f(x)=g(x)h(x)$ for some polynomials $f,g,h$ with matrix coefficients, we don’t have $f(M)=g(M)h(M)$ for an arbitrary matrix $M$. Here you have $f(C)=g(C)h(C)$ because all coefficients of $g$ commute with $C$. As the author wrote, this is relevant to his proof of Cayley-Hamilton theorem. See also the discussion in my recent answer. – user1551 Aug 17 '24 at 18:55
  • @user1551 thank you very much for your comment! – 佐武五郎 Aug 18 '24 at 04:35

1 Answers1

1

The variable $x$ is a scalar variable, not a matrix variable. This is very important to remember when working with polynomial matrices. If we take a true identity involving polynomial matrices, and substitute some number for $x$, we will obtain a true matrix identity. But is is not true if we substitute a matrix for $x$.

Consider the following simple example: it is true that $$\begin{bmatrix}1 & 0 \\ 0 & 0\end{bmatrix}x \cdot \begin{bmatrix}0 & 0 \\ 0 & 1\end{bmatrix} x = 0$$ but if we try to substitute a matrix $\begin{bmatrix}0 & 1 \\ 1 & 0\end{bmatrix}$ for $x$, we get $$\begin{bmatrix}1 & 0 \\ 0 & 0\end{bmatrix} \begin{bmatrix}0 & 1 \\ 1 & 0\end{bmatrix} \cdot \begin{bmatrix}0 & 0 \\ 0 & 1\end{bmatrix} \begin{bmatrix}0 & 1 \\ 1 & 0\end{bmatrix} = \begin{bmatrix}1 & 0 \\ 0 & 0\end{bmatrix} \neq 0$$

Vladimir Lysikov
  • 3,745