Evaluate series of exponential divided by 1st order polynomial (residue theorem?)

Question

While investigating the dynamics of a frequency modulated quantum system I came across this innocently looking series: $$\sum_{n=-\infty}^{\infty} \frac{e^{i n \theta}}{\mu+n} \tag{1},$$ where $\mu \in \mathbb{C}$ and $\theta \in \mathbb{R}$, I tried solving it with the residue theorem assuming that a contour integral enclosing all poles of $$\pi \cot {\pi z} \frac{e^{i z \theta}}{\mu+z} ,\tag{2}$$ equals zero, so then the series in Eq. $(1)$ would equal minus the residue of Eq. $(2)$ at the pole $z=-\mu$, i.e., $$-\pi \cot({-\pi \mu}) e^{-i \mu \theta} \tag{3}.$$

However, when Fourier series expanding this result in Mathematica, it doesn't look quite like the original series. Therefore, I wonder if for example the assumption that the contour integral is zero is wrong (e.g., because of exponential growth being faster than polynomial) and how to calculate it. I'm a physicist and thus my complex analysis skills are quite limited.

Any hints?

Answer 1

Here is another method for performing the sum. We take $\Re (\mu)$ to not be an integer and take $\theta$ to not be equal to $k2 \pi$ for $k \in \mathbb{Z}$.

First we take $0 < \Re (\mu) < 1$. For later convenience, note $\theta= 2 \pi (\frac{\theta}{2 \pi}) = 2 \pi (\lfloor \frac{\theta}{2 \pi} \rfloor + \{ \frac{\theta}{2 \pi} \})$ where $\lfloor \cdots \rfloor$ is the floor function and $\{ \frac{\theta}{2 \pi} \}$ is the fractional part of $\frac{\theta}{2 \pi}$.

We have

\begin{align*} & \sum_{n=-\infty}^\infty \frac{e^{i n \theta}}{\mu + n} \nonumber \\ & = \frac{1}{\mu} + \sum_{n=1}^\infty \frac{e^{i n \theta}}{\mu + n} - \sum_{n=1}^\infty \frac{e^{-i n \theta}}{-\mu + n} \nonumber \\ & = \frac{1}{\mu} + \sum_{n=1}^\infty \frac{e^{i n \theta}}{\mu + n} \int_0^\infty e^{-u} du - \sum_{n=1}^\infty \frac{e^{-i n \theta}}{-\mu + n} \int_0^\infty e^{-u} du \nonumber \\ & = \frac{1}{\mu} + \sum_{n=1}^\infty \int_0^\infty e^{-u (n+\mu) + in \theta} du - \sum_{n=1}^\infty \int_0^\infty e^{-u (n -\mu) - in \theta} du \nonumber \\ & = \frac{1}{\mu} + \int_0^\infty \sum_{n=1}^\infty e^{-n (u - i \theta)} e^{-u \mu} du - \int_0^\infty \sum_{n=1}^\infty e^{-n (u+ i\theta)} e^{u \mu} du \nonumber \\ & = \frac{1}{\mu} + \int_0^\infty \frac{e^{-u \mu}}{e^{u - i \theta} - 1} du - \int_0^\infty \frac{e^{u \mu}}{e^{u + i \theta} - 1} du \nonumber \\ & = \frac{1}{\mu} + \left[ - \frac{1}{\mu} \frac{e^{-u \mu}}{e^{u - i \theta} - 1} \right]_0^\infty - \frac{1}{\mu} \int_0^\infty \frac{e^{-u \mu} e^{u - i \theta}}{(e^{u - i \theta} - 1)^2} du - \left[ \frac{1}{\mu} \frac{e^{u \mu}}{e^{u + i \theta} - 1} \right]_0^\infty - \frac{1}{\mu} \int_0^\infty \frac{e^{u \mu} e^{u + i \theta}}{(e^{u + i \theta} - 1)^2} du \nonumber \\ & = \frac{1}{\mu} + \frac{1}{\mu} \frac{1}{e^{- i \theta} - 1} + \frac{1}{\mu} \frac{1}{e^{i \theta} - 1} - \frac{1}{\mu} \int_0^\infty \frac{e^{-u \mu} e^{u + i \theta}}{(e^u - e^{i \theta})^2} du - \frac{1}{\mu} \int_0^\infty \frac{e^{u \mu} e^{u - i \theta}}{(e^u - e^{-i \theta})^2} du \nonumber \\ & = - \frac{1}{\mu} \int_{-\infty}^\infty \frac{e^{-u \mu} e^u e^{i \theta}}{(e^u - e^{i \theta})^2} du \end{align*}

where we have done an integration by parts and the substitution $u \rightarrow - u$ in the second integral in the second to last line (strictly, you need to justify the step where a summation and integration were interchanged). Consider the rectangular contour in the figure

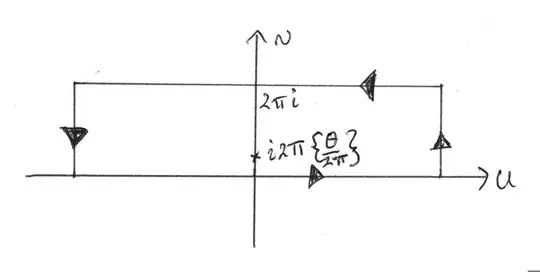
and contour integral:

\begin{align*} \oint \frac{e^{-z \mu} e^z e^{i \theta}}{(e^z - e^{i \theta})^2} dz \end{align*}

The whose integrand has pole at $i 2 \pi \{ \frac{\theta}{2 \pi} \}$. The integral along the vertical edges vanishes as:

\begin{align*} f(z) = \dfrac{e^{(-\mu+1) (u+iv)} e^{i \theta}}{(e^{u+iv} + e^{i \theta})^2} = \begin{cases} e^{i \theta} e^{(-\mu - 1) (u+iv)} & u \rightarrow \infty \\ e^{-i \theta} e^{(-\mu+1) (u+iv)} & u \rightarrow - \infty \\ \end{cases} \end{align*}

So that

\begin{align*} & e^{i \theta} \oint_C \dfrac{e^{-\mu z}}{(e^z - e^{i \theta})^2}dz \nonumber \\ & = e^{i \theta} \int_{-\infty}^\infty \dfrac{e^{-\mu u}}{(e^u - e^{i \theta})^2} du - e^{i \theta} e^{- \mu 2 \pi i} \int_{-\infty + 2 \pi i}^{\infty + 2 \pi i} \dfrac{e^{- \mu u}}{(e^u - e^{i \theta})^2} du \nonumber \\ & = (1-e^{-\mu 2 \pi i}) e^{i \theta} \int_{-\infty}^\infty \dfrac{e^{-\mu u}}{(e^u - e^{i \theta})^2} du \end{align*}

We arrive a

\begin{align*} \int_{-\infty}^\infty \dfrac{e^{i \theta} e^{-\mu u} e^u}{(e^u - e^{i \theta})^2} du & = \frac{2 \pi i }{1-e^{-\mu 2 \pi i}} \frac{1}{2 \pi i} \oint_C \dfrac{e^{i \theta} e^{-\mu z} e^z}{(e^z - e^{i 2 \pi \{ \frac{\theta}{2 \pi} \}})^2} dz \nonumber \\ & = \frac{2 \pi i}{1-e^{-\mu 2 \pi i}} Res [f(z)] \end{align*}

We wish to expand the integrand in powers of $z-z_0$ about the pole $z_0= i 2 \pi \{ \frac{\theta}{2 \pi} \}$. First note:

\begin{align*} \frac{1}{(e^z - e^{z_0})^2} & = \frac{e^{-2 z_0}}{(e^{z-z_0} - 1)^2} \nonumber \\ & = \frac{e^{-2 z_0}}{[z-z_0 + \frac{1}{2!} (z-z_0)^2 + \cdots]^2} \nonumber \\ & = \frac{e^{-2 z_0}}{(z-z_0)^2 [1 + \frac{1}{2!} (z-z_0) + \cdots]^2} \nonumber \\ & = \dfrac{e^{-2z_0}}{(z-z_0)^2} - \dfrac{e^{-2z_0}}{z-z_0} + \cdots \end{align*}

Then note:

\begin{align*} \dfrac{e^{z_0} e^{-\mu z} e^z}{(e^z - e^{z_0})^2} & = e^{-z_0} \dfrac{ e^{(-\mu + 1) z_0 + (-\mu + 1) (z-z_0)} }{ (z-z_0)^2 } - e^{-z_0} \dfrac{ e^{(-\mu + 1) z_0} }{ z-z_0 } + \cdots \nonumber \\ & = e^{-z_0} \dfrac{ e^{(-\mu + 1) z_0} [1 + (-\mu + 1) (z-z_0) + \cdots] }{ (z-z_0)^2 } - e^{-z_0} \dfrac{ e^{(-\mu + 1) z_0} }{ z-z_0 } + \cdots \nonumber \\ & = \dfrac{ e^{-\mu z_0} }{ (z-z_0)^2 } + \dfrac{ -\mu e^{-\mu z_0} }{ z-z_0 } + \cdots \end{align*}

Combining everything

\begin{align*} \int_{-\infty}^\infty \dfrac{e^{i \theta} e^{-\mu u}}{(e^u - e^{i \theta})^2} du & = \pi \frac{2i}{1-e^{-\mu 2 \pi i}} \cdot -\mu e^{-\mu i 2 \pi \{ \frac{\theta}{2 \pi} \}} \nonumber \\ & = - e^{-\mu i 2 \pi \{ \frac{\theta}{2 \pi} \} + \mu \pi i} \dfrac{\mu \pi}{\sin \mu \pi} \end{align*}

Finally, for the case where $0 < \Re (\mu) < 1$, we have

\begin{align*} \sum_{n=-\infty}^\infty \frac{e^{i n \theta}}{\mu + n} = e^{-\mu i 2 \pi \{ \frac{\theta}{2 \pi} \} + \mu \pi i} \dfrac{\pi}{\sin \mu \pi} \end{align*}

Now consider the general case where $\mu = m + \{ \mu_R \} + i \mu_I$ with $0 < \{ \mu_R \} < 1$. Then

\begin{align*} \sum_{n=-\infty}^\infty \frac{e^{i n \theta}}{\mu + n} & = \sum_{n=-\infty}^\infty \frac{e^{i n \theta}}{\{ \mu_R \} + m + i \mu_I + n} \nonumber \\ & = e^{-i m \theta} \sum_{n=-\infty}^\infty \frac{e^{i (n+m) \theta}}{\{ \mu_R \} + i \mu_I + (m+n)} \nonumber \\ & = e^{-i m 2 \pi \{ \frac{\theta}{2 \pi} \}} \sum_{n=-\infty}^\infty \frac{e^{i n \theta}}{\{ \mu_R \} + i \mu_I + n} \nonumber \\ & = e^{-i m 2 \pi \{ \frac{\theta}{2 \pi} \}} e^{-(\{ \mu_R \} + i\mu_I) i 2 \pi \{ \frac{\theta}{2 \pi} \} + (\{ \mu_R \} + i\mu_I) \pi i} \dfrac{\pi}{\sin (\{ \mu_R \} + i\mu_I) \pi} \nonumber \\ & = (-1)^m e^{-\mu i 2 \pi \{ \frac{\theta}{2 \pi} \} + \mu \pi i} \dfrac{\pi}{\sin (\{ \mu_R \} + i\mu_I) \pi} \nonumber \\ & = e^{-\mu i 2 \pi \{ \frac{\theta}{2 \pi} \} + \mu \pi i} \dfrac{\pi}{\sin \mu \pi} \end{align*}

where I have used the trig identity $\sin (-m \pi + \mu \pi) = \cos (-m \pi) \sin \mu \pi = (-1)^m \sin \mu \pi$.

Check: taking the derivative with respect to $\theta$ ($\theta \not=k 2\pi$):

\begin{align*} \frac{d}{d \theta} \sum_{n=-\infty}^\infty \frac{e^{i n \theta}}{\mu + n} = \frac{d}{d \theta} f(\theta) = -i \mu e^{-\mu i 2 \pi \{ \frac{\theta}{2 \pi} \} + \mu \pi i} \dfrac{\pi}{\sin \mu \pi} = -i \mu f(\theta) \end{align*}

Answer 2

The issue is indeed that the contour integral does not vanish.

If $ \theta >0$, then the magnitude of $e^{i z \theta}$ grows exponentially as $\Im(z) \to -\infty$.

And if $\theta <0$, then the magnitude of $e^{iz \theta}$ grows exponentially as $\Im(z) \to + \infty.$

However, we can modify the integrand so that the contour integral does vanish in the case that $0 < \theta < 2 \pi$.

Consider the function $$f(z) = \pi \left(\cot(\pi z) -i \right) \frac{e^{i z \theta}}{\mu + z} = \frac{\pi}{\sin (\pi z)} \frac{e^{i(\theta - \pi)z}}{\mu +z}, \quad \color{red}{0 < \theta < 2 \pi},$$

and a rectangular contour with vertices at $$z= \pm (N+1/2)\pm i\sqrt{N} ,$$ where $N$ is some large positive integer.

As $N \to \infty$, the integrals along the left and right sides of the contour vanish because $$ \left| \frac{e^{i(\theta - \pi)(\pm(N+1/2)+it)}}{\sin(\pi (\pm (N+1/2)+it))} \right| = \frac{e^{(\pi - \theta)t}}{\cosh(\pi t)} \le 2 $$ for any $- \sqrt{N} < t < \sqrt{N}$ when $0 < \theta < 2 \pi$.

And the integrals along the top and bottom of the contour vanish as $N \to \infty$ because the magnitude of $$\frac{e^{i(\theta - \pi)z}}{\sin(\pi z)} $$ decays exponentially to zero as $\Im(z) \to \pm \infty$ when $0 < \theta < 2 \pi$.

We therefore have $$ \begin{align} 0 &= 2 \pi i \left(\sum_{n=-\infty}^{\infty} \operatorname*{Res}_{z= n} f(z) + \operatorname*{Res}_{z = - \mu} f(z)\right) \\ &= 2 \pi i \left(\sum_{n=-\infty}^{\infty} \frac{e^{i n \theta}}{\mu +n} - \frac{\pi}{\sin(\pi \mu)} e^{i \mu(\pi - \theta)}\right), \end{align}$$

from which it follows that $$\sum_{n=-\infty}^{\infty} \frac{e^{i n \theta}}{\mu +n} = \frac{\pi}{\sin(\pi \mu)} e^{i \mu(\pi - \theta)}, \quad 0 < \theta < 2 \pi.$$

This agrees with Dave77's generalized result.

Answer 3

This kind of summation is usually represented with the help of Lerch transcendent / Hurwitz zeta function, defined as $$ \Phi(z,s,a) = \sum_{n\in\Bbb{Z}} \frac{z^n}{(n+a)^s}. $$ It is convergent for $|z| < 1$ or $|z| = 1$ with $\operatorname{Re}(s) > 1$ only. In consequence, the quantity $$ f(\theta) = \sum_{n\in\Bbb{Z}} \frac{e^{in\theta}}{n+\mu} $$ doesn't converge for any $\theta \in \Bbb{R}$, that is why you may consider its analytic continuation on the complex plane instead. What to do next ? Even if the Lerch/Hurwitz function permits to link $f$ to a special function, does the latter admit another (more practical) form ? In fact, it satisfies to a simple differential equation, namely $$ f'(\theta) = -i\mu f(\theta) + 2\pi i\, \delta(\theta), $$ where we used the Fourier series representation of the Dirac delta function, i.e. $$ \delta(\theta) = \frac{1}{2\pi} \sum_{n\in\Bbb{Z}} e^{in\theta}. $$ One understands thus that $f$ behaves like the antiderivative of the Dirac delta function, that is the Heaviside function, together with a complex exponential, which is responsible for the translation by $\mu$ in the Fourier series. However, you won't be able to determine a suitable constant of integration on the real line because of the aforementioned divergence issues. Nevertheless, you may use representations of Dirac/Heaviside functions on the complex plane and integrate the differential equation along a curve in the said complex plane.