Find the exact value of $\int_{0}^{2}x[\frac{1}{x}]dx$.

Question

Find the exact value of $\int_{0}^{2}x\left[\frac{1}{x}\right]dx$.

Let $[x]$ denote $\lceil{x-\frac{1}{2}}\rceil$.

Using Desmos, I got $2.46736022133$ and WolframAlpha does not give me a solution. My intuition tells me that it might be possible to find an exact value using Trapezoidal Reimann Sums but I am not really sure how to go about doing it. After my attempt, I got stuck but I was at a point where I could plug it into WolframAlpha and it gave me $\frac{\pi^2}{4}$. Why did it come out so nicely?

My attempt:

Where $A_n$ denotes the area of the $nth$ trapezoid from the right: $$A=\frac{h}{2}(a+b)$$ $$A_n=\frac{\frac{2}{2n-1}-\frac{2}{2n+1}}{2}(\frac{2n}{2n-1}+\frac{2n}{2n+1})$$ $$A_n=\frac{\frac{4n+2}{4n^{2}-1}-\frac{4n-2}{4n^{2}-1}}{2}\left(\frac{4n^{2}+2n}{4n^{2}-1}+\frac{4n^{2}-2n}{4n^{2}-1}\right)$$ $$A_n=\frac{2}{4n^{2}-1}\left(\frac{8n^{2}}{4n^{2}-1}\right)$$ $$A_n=\frac{16n^{2}}{\left(4n^{2}-1\right)^{2}}$$

Then: $$\int_{0}^{2}x\left[\frac{1}{x}\right]dx=\sum_{n=1}^{\infty}A_n=\sum_{n=1}^{\infty}\frac{16n^{2}}{\left(4n^{2}-1\right)^{2}}$$ I do not know how to solve this infinite summation so I plugged it into WolframAlpha and it gave me $\frac{\pi^2}{4}$. How did it get to this conclusion? Is there a more efficient way to solve this?

Answer 1

Continuing where you left off. Note \begin{align*} &\sum_{n=1}^\infty\frac{16n^2}{4n^2-1} \\ &= 2\sum_{n=1}^\infty n\left(\frac{1}{(2n-1)^2} - \frac{1}{(2n+1)^2}\right)\\ &= 2\sum_{n=1}^\infty \left(\sum_{k=1}^n 1\right) \left(\frac{1}{(2n-1)^2} - \frac{1}{(2n+1)^2}\right)\\ &= 2\sum_{n=1}^\infty \sum_{k=1}^n \left(\frac{1}{(2n-1)^2} - \frac{1}{(2n+1)^2}\right)\\ &= 2\sum_{k=1}^\infty \sum_{n=k}^\infty \left(\frac{1}{(2n-1)^2} - \frac{1}{(2n+1)^2}\right)\\ &= 2\sum_{k=1}^\infty \sum_{n=k}^\infty \left(\frac{1}{(2n-1)^2}\right) - \sum_{n=k+1}^\infty\left(\frac{1}{(2n-1)^2}\right)\\ &= 2\sum_{k=1}^\infty \frac{1}{(2k-1)^2} \\ &= 2\left(\sum_{k=1}^\infty \frac{1}{k^2} - \sum_{k=1}^\infty \frac{1}{(2k)^2}\right) \\ &= 2\cdot\frac{3}{4}\sum_{k=1}^\infty\frac{1}{k^2} \\ &= 2\cdot\frac{3}{4}\cdot\frac{\pi^2}{6} = \frac{\pi^2}{4} \end{align*}

Answer 2

• If $[x]:=n$ iff $n-\tfrac12< x\leq n+\tfrac12$ (i.e. $[x]=\lceil x-\tfrac12\rceil$, which seems to be what the OP had in mind), then \begin{align} \int^2_0 x[1/x]\,dx & =\sum^\infty_{n=1}\int_{[\tfrac{2}{2n+1},\tfrac2{2n-1})}nx\,dx\\ &=\sum^\infty_{n=1}\Big(\frac{2n-1+1}{(2n-1)^2}-\frac{2n+1-1}{(2n+1)^2}\Big)\\ &=\sum^\infty_{n=1}\Big(\frac{1}{2n-1}-\frac{1}{2n+1}+\frac{1}{(2n-1)^2}+\frac{1}{(2n+1)^2}\Big)\\ &=1+2\sum^\infty_{n=1}\frac{1}{(2n-1)^2}-1=2\Big(\sum^\infty_{n=1}\frac{1}{n^2}-\frac14\sum^\infty_{n=1}\frac1{n^2}\Big)\\ &=\frac{\pi^2}{4} \end{align}

• The same estimate holds when $[x]:=n$ iff $n-\tfrac12 \leq x<n+\tfrac12$ (i.e., $[x]=\lfloor x+\tfrac12\rfloor$) since $\lceil x-\tfrac12\rceil=\lfloor x+\tfrac12\rfloor$ a.s.

---

• If by $[\cdot]$ the OP means the ceiling function $\lceil x\rceil=n$ where $n-1<x\leq n$, then $$\int^2_0 x\lceil 1/x \rceil\,dx=\int^1_0 x\lceil 1/x \rceil\,dx +\int^2_1 x\,dx=\int^1_0 x\lceil 1/x\rceil \,dx + \frac32$$ From \begin{align} \int^1_0 x\lceil 1/x \rceil\,dx & =\sum^\infty_{n=2}\int_{[\tfrac{1}{n},\tfrac1{n-1})}nx\,dx=\sum^\infty_{n=2}\frac{n}{2}\Big(\frac{1}{(n-1)^2}-\frac{1}{n^2}\Big)\\ &=\sum^\infty_{n=2}\frac{2n-1}{2n(n-1)^2}=\sum^\infty_{n=2}\frac{1}{(n-1)^2}+\frac{n-1-n}{2n(n-1)^2}\\ &=\frac12\sum^\infty_{n=1}\frac{1}{n^2}+\frac12\sum^\infty_{n=2}\frac{1}{n(n-1)} =\frac{\pi^2}{12}+\frac12 \end{align} The value of the integral in this case is $\frac{\pi^2}{12}+2\approx 2.822467$

• If the OP means $[\cdot]$ to be the integer part function (floor function) $\lfloor x\rfloor =n$ iff $n\leq x<n+1$, then $$\int^2_0 x\lfloor 1/x \lfloor\,dx=\int^1_0 x\lfloor 1/x \rfloor\,dx +\int^2_1 0\cdot x\,dx=\int^1_0 x\lfloor 1/x\rfloor \,dx $$ The value of the integral is then given by \begin{align} \int^1_0 x\lfloor 1/x \rfloor\,dx & =\sum^\infty_{n=1}\int_{(\tfrac{1}{n+1},\tfrac1n]}nx\,dx=\sum^\infty_{n=1}\frac{n}{2}\Big(\frac{1}{n^2}-\frac{1}{(n+1)^2}\Big)\\ &=\sum^\infty_{n=1}\frac{2n+1}{2n(n+1)^2}=\sum^\infty_{n=1}\frac{1}{(n+1)^2}+\frac{n+1-n}{2n(n+1)^2}\\ &=\frac12\sum^\infty_{n=2}\frac{1}{n^2}-\frac12\sum^\infty_{n=1}\frac{1}{n(n+1)} =\frac{\pi^2}{12} \end{align}

Answer 3

An alternate solution:

$$ \begin{align} \int_{0}^{2}x\operatorname{round}\left(\frac{1}{x}\right)dx &= \int_0^2 x\Biggl\lfloor{\frac{1}{x}+\frac{1}{2}\Biggr\rfloor}dx \tag{1}\\ &= 8\int_{1}^{\infty}\frac{\lfloor{x\rfloor}}{\left(2x-1\right)^{3}}dx \tag{2}\\ &= 8\sum_{n=1}^{\infty}n\int_{n}^{n+1}\frac{dx}{\left(2x-1\right)^{3}} \\ &= 16\sum_{n=1}^{\infty}\frac{n^{2}}{\left(1-4n^{2}\right)^{2}} \\ \end{align} $$

where in $(1)$ we used the Desmos interpretation $\displaystyle \operatorname{round}\left(\frac{1}{x}\right) := \Biggl\lfloor{\frac{1}{x}+\frac{1}{2}\Biggr\rfloor}$ and in $(2)$ we used the mapping $\displaystyle \frac{1}{x}+\frac{1}{2} \mapsto x$.

Next, let $f$ be a piecewise smooth function on $[0,L]$. Then the Fourier sine expansion is given by

$$f\left(x\right)\ =\ \sum_{n=1}^{\infty}b_{n}\sin\left(\frac{\pi nx}{L}\right)$$

where we have the sequence

$$b_{n}=\frac{2}{L}\int_{0}^{L}f\left(x\right)\sin\left(\frac{\pi nx}{L}\right)dx.$$

Let $f(x) = \cos(x)$ and $L = \dfrac{\pi}{2}$. Then using some basic integration, we can prove that

$$b_{n}=\frac{4}{\pi}\int_{0}^{\frac{\pi}{2}}\cos\left(x\right)\sin\left(2nx\right)dx\ =\ \frac{4}{\pi}\cdot\frac{2n}{4n^{2}-1}.$$

This means

$$ \begin{align} \cos\left(x\right) &= \frac{4}{\pi}\sum_{n=1}^{\infty}\frac{2n}{4n^{2}-1}\sin\left(2nx\right) \\ \implies \cos^2(x) &= \frac{8}{\pi}\sum_{n=1}^{\infty}\frac{n\cos\left(x\right)\sin\left(2nx\right)}{4n^{2}-1} \\ \implies \int_{0}^{\frac{\pi}{2}}\cos^{2}\left(x\right)dx &= \frac{8}{\pi}\sum_{n=1}^{\infty}\frac{n}{4n^{2}-1}\int_{0}^{\frac{\pi}{2}}\cos\left(x\right)\sin\left(2nx\right)dx \\ &= \frac{8}{\pi}\sum_{n=1}^{\infty}\frac{n}{4n^{2}-1}\cdot\frac{2n}{4n^{2}-1}. \\ &= \frac{16}{\pi}\sum_{n=1}^{\infty}\frac{n^{2}}{\left(4n^{2}-1\right)^{2}} \\ \end{align} $$

But $\displaystyle \int_{0}^{\frac{\pi}{2}}\cos^{2}\left(x\right)dx=\frac{\pi}{4}$. By transitivity, we get

$$\frac{\pi}{4}=\frac{16}{\pi}\sum_{n=1}^{\infty}\frac{n^{2}}{\left(4n^{2}-1\right)^{2}}.$$

Therefore,

$$\int_{0}^{2}x\operatorname{round}\left(\frac{1}{x}\right)dx = \frac{\pi^{2}}{4}.$$

Answer 4

$$\frac{16 n^2}{\left(4 n^2-1\right)^2}=-\frac{1}{2 n+1}+\frac{1}{(2 n+1)^2}+\frac{1}{2 n-1}+\frac{1}{(2 n-1)^2}$$ $$\sum_{n=1}^p\frac{16 n^2}{\left(4 n^2-1\right)^2}=\frac{1}{2} \left(\psi ^{(0)}\left(\frac{3}{2}\right)-\psi ^{(0)}\left(p+\frac{3}{2}\right)\right)+$$ $$\frac{1}{8} \left(-2 \psi ^{(1)}\left(p+\frac{3}{2}\right)+\pi ^2-8\right)+$$ $$\frac{1}{2} \left(\psi ^{(0)}\left(p+\frac{1}{2}\right)-\psi ^{(0)}\left(\frac{1}{2}\right)\right)+ \frac{1}{8} \left(\pi ^2-2 \psi ^{(1)}\left(p+\frac{1}{2}\right)\right)$$

Using the asymptotics $$\sum_{n=1}^p\frac{16 n^2}{\left(4 n^2-1\right)^2}=\frac{\pi ^2}{4}-\frac{1}{p}+\frac{1}{2 p^2}+O\left(\frac{1}{p^3}\right)$$

Answer 5

Another way to get the sum of the series $$\sum_{n=1}^{\infty} \frac{16n^2}{(4n^2-1)^2} $$ without double summations and without switching the order of the sums. \begin{align} \sum_{n=1}^N \frac{16n^2}{(4n^2-1)^2} &= \sum_{n=1}^N \left[ \frac{2n}{(2n-1)^2} - \frac{2n}{(2n+1)^2} \right] \\[2pt] &= 2 \sum_{n=1}^N \frac1{(2n-1)^2} + \sum_{n=1}^N \left[ \frac{2(n-1)}{(2n-1)^2} - \frac{2n}{(2n+1)^2} \right] \\[2pt] &= 2 \left( \sum_{n=1}^{2N-1} \frac1{n^2} - \sum_{n=1}^{N-1} \frac1{(2n)^2} \right) + \left[ 0 - \frac2{3^2} + \frac2{3^2} -\frac4{5^2} + \dots{} \right. \\[2pt] &\quad+ \left. \frac{2(N-1)}{(2N-1)^2} - \frac{2N}{(2N+1)^2} \right] \\[2pt] &= 2 \left( \sum_{n=1}^{2N-1} \frac1{n^2} - \frac14 \sum_{n=1}^{N-1} \frac1{n^2} \right) - \frac{2N}{(2N+1)^2}\,. \end{align}

Hence, \begin{align} \sum_{n=1}^{\infty} \frac{16n^2}{(4n^2-1)^2} &= \lim_{N\to\infty} \left[ \sum_{n=1}^N \frac{16n^2}{(4n^2-1)^2} \right] \\[2pt] &= \lim_{N\to\infty}\left[2\left(\sum_{n=1}^{2N-1}\frac1{n^2}-\frac14\sum_{n=1}^{N-1}\frac1{n^2}\right)-\frac{2N}{\left(2N+1\right)^2}\right] \\[2pt] &= 2 \left( \sum_{n=1}^{\infty} \frac1{n^2} -\frac14 \sum_{n=1}^{\infty} \frac1{n^2} \right) \\[2pt] &= 2 \left( \frac{\pi^2}6 - \frac14\!\cdot\!\frac{\pi^2}6 \right) \\[2pt] &= 2 \left(1 - \frac14\right) \frac{\pi^2}6 \\[2pt] &= 2 \!\cdot\! \frac34\!\cdot\! \frac{\pi^2}6 \\[2pt] &= \frac{\pi^2}4\,. \end{align}

Answer 6

Here is a crazy and over-the-top method using contour integration.

$$ \bbox[15px,#FFFAFD,border:6px groove #0712FF ]{\int_0^2 x \Biggl\lceil{\frac{1}{x}-\frac{1}{2}\Biggl\rceil}dx = \frac{\pi^2}{4}} $$

---

PROOF. Let the integral equal $\mathcal{I}$. Using the transformation $\displaystyle \frac{1}{x}+\frac{1}{2} \mapsto x$, we get

$$ \begin{align} \mathcal{I} &= \int_0^2 x \Biggl\lceil{\frac{1}{x}-\frac{1}{2}\Biggl\rceil}dx \\ &= \int_0^2 x \Biggl\lfloor{\frac{1}{x}+\frac{1}{2}\Biggl\rfloor}dx \\ &\overset{\frac{1}{x}+\frac{1}{2} \mapsto x}= 8\int_{1}^{\infty}\frac{\lfloor{x\rfloor}}{\left(2x-1\right)^{3}}dx \\ &= 8\sum_{k \in \mathbb{Z}^+} k\int_{k}^{k+1}\frac{dx}{\left(2x-1\right)^{3}} \\ &= 16\sum_{k \in \mathbb{Z}^+}\frac{k^{2}}{\left(4k^{2}-1\right)^{2}} \\ &= 8\sum_{k \in \mathbb{Z}}\frac{k^{2}}{\left(4k^{2}-1\right)^{2}}\,. \\ \end{align} $$

In that last equality, note that the sequence of terms $\displaystyle \frac{k^2}{(4k^2-1)^2}$ for negative $k$ equals that of positive $k$.

---

We define a function $\displaystyle f: \mathbb{C} \,\backslash \left(\mathbb{Z}^+ \cup \mathbb{Z}^- \cup \left\{-\frac{1}{2},\frac{1}{2}\right\}\right) \to \mathbb{C}$ such that $\displaystyle z \mapsto \frac{z^2 \cot(\pi z)}{(4z^2-1)^2}$. We also construct a counterclockwise circular contour and a set of poles

$$ \begin{align} C_n &:= \left\{t \in [0,2\pi]\,:\,\left(n+\frac{1}{2}\right)e^{it}\right\} \\ \mathcal{P}_n &:= \overbrace{\left(\left\{-n,-n+1,\ldots,n-1,n\right\}\,\backslash \left\{0\right\}\right) \cup \left\{-\frac{1}{2},\frac{1}{2}\right\}}^\text{set of simple poles} \end{align} $$

where $n \in \mathbb{Z}^+$. The visual above depicts the contour $C_n$ enclosing $\mathcal{P}_n$ over the rainbow phase plot of $f$ with shading.

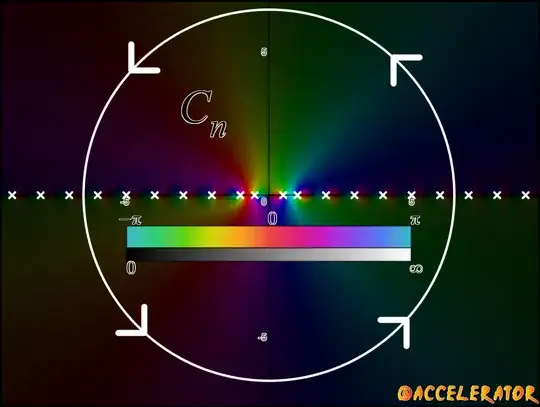
Notice that $z=0$ is a removable singularity. Writing $\displaystyle \frac{z}{e^{\pi iz}-1}$ as an asymptotic Taylor expansion centered at $z=0$, we get

$$ \begin{align} f(z) &= \frac{z^2\cot(\pi z)}{(4z^2-1)^2} \\ &= \frac{iz\left(1+e^{2\pi iz}\right)}{\left(4z^{2}-1\right)^{2}\left(e^{\pi iz}+1\right)}\cdot\frac{z}{e^{\pi iz}-1} \\ &= \frac{iz\left(1+e^{2\pi iz}\right)}{\left(4z^{2}-1\right)^{2}\left(e^{\pi iz}+1\right)}\cdot\left(-\frac{i}{\pi}-\frac{1}{2}z+\frac{i\pi}{12}z^{2}+\mathcal{O}\left(z^{4}\right)\right)\,. \end{align} $$

This expansion makes it possible to redefine $f$ such that it's analytic in a neighborhood of $0$ and remove $z=0$ as a singularity.

Employing Cauchy's Residue Theorem, we get

$$ \oint_{C_n}f(z)dz = 2\pi i\sum_{k \,\in\, P_n}\mathop{\mathrm{Res}}_{z\,=\,k}f(z) = 2\pi i \left(\sum_{k\,=\,-n}^{n}\mathop{\mathrm{Res}}_{z\,=\,k} f(z) +\mathop{\mathrm{Res}}_{z\,=\,-\frac{1}{2}}f(z) + \mathop{\mathrm{Res}}_{z\,=\,\frac{1}{2}}f(z)\right) $$

---

Evaluating the residue at $\displaystyle z=-\frac{1}{2}$ of $f(z)dz$, we get

$$ \begin{align} 2\pi i\mathop{\mathrm{Res}}_{z\,=\,-\frac{1}{2}}f(z) &= 2\pi i \lim_{z\,\to\,-\frac{1}{2}}\left(z+\frac{1}{2}\right)\cdot\frac{iz^{2}\left(1+e^{2\pi iz}\right)}{16\left(z-\frac{1}{2}\right)^{2}\left(z+\frac{1}{2}\right)^{2}\left(e^{2\pi iz}-1\right)} \\ &= -\frac{\pi}{8}\lim_{z\,\to\,-\frac{1}{2}}\frac{z^{2}}{\left(z-\frac{1}{2}\right)^{2}\left(e^{2\pi iz}-1\right)} \lim_{z\,\to\,-\frac{1}{2}}\frac{1+e^{2\pi iz}}{z+\frac{1}{2}} \\ &= -\frac{\pi}{8}\cdot\frac{\left(-\frac{1}{2}\right)^{2}}{\left(-\frac{1}{2}-\frac{1}{2}\right)^{2}\left(e^{2\pi i\left(-\frac{1}{2}\right)}-1\right)}\cdot \lim_{z\,\to\,-\frac{1}{2}}\frac{\frac{d}{dz}\left(1+e^{2\pi iz}\right)}{\frac{d}{dz}\left(z+\frac{1}{2}\right)} \\ &= \frac{\pi}{64}\lim_{z\,\to\,-\frac{1}{2}}\frac{2\pi ie^{2\pi iz}}{1} \\ &= \frac{\pi}{64}\cdot2\pi ie^{2\pi i\left(-\frac{1}{2}\right)} \\ &= -\frac{i\pi^{2}}{32}\,. \\ \end{align} $$

The same process should apply for calculating the residue at $\displaystyle z=\frac{1}{2}$. It should be

$$ 2\pi i\mathop{\mathrm{Res}}_{z\,=\,\frac{1}{2}}f(z) = -\frac{i\pi^2}{32}\,. $$

Calculating the rest of the residues, we get

$$ \begin{align} 2\pi i \sum_{k\,=\,-n}^{n}\mathop{\mathrm{Res}}_{z\,=\,k} f(z) &= 2\pi i \lim_{z\,\to\,k} \frac{iz^{2}\left(1+e^{2\pi iz}\right)}{\frac{d}{dz}\left(4z^{2}-1\right)^{2}\left(e^{2\pi iz}-1\right)}\\ &= -2\pi\sum_{k\,=\,-n}^{n}\lim_{z\,\to\,k}\frac{z^{2}\left(1+e^{2\pi iz}\right)}{2\left(4z^{2}-1\right)\left(4\pi iz^{2}e^{2\pi iz}+8ze^{2\pi iz}-8z-i\pi e^{2\pi iz}\right)}\\ &=-2\pi\sum_{k=-n}^{n}\frac{k^{2}\left(1+e^{2\pi ik}\right)}{2\left(4k^{2}-1\right)\left(4\pi ik^{2}e^{2\pi ik}+8ke^{2\pi ik}-8k-i\pi e^{2\pi ik}\right)} \tag{1}\\ &= 2i\sum_{k=-n}^{n}\frac{k^{2}}{\left(4k^{2}-1\right)^{2}}\,. \\ \end{align} $$

In $(1)$, we use the piecewise equality

$$ e^{k\pi i} = \begin{cases} 1 & k \equiv 0 \pmod{2} \\ -1 & k \equiv 1 \pmod{2}\,. \\ \end{cases} $$

Equating the imaginary part on both sides of the equality that resulted from Cauchy's Residue Theorem and applying $n \to \infty$, we recover the infinite series we want as follows:

$$ \lim_{n\,\to\,\infty}\Im\oint_{C_n}\frac{z^{2}\cot\left(\pi z\right)}{\left(4z^{2}-1\right)^{2}} = \sum_{k\,\in\,\mathbb{Z}}\frac{2k^{2}}{\left(4k^{2}-1\right)^{2}} - \frac{\pi^{2}}{16} $$

$$ \implies \sum_{k\,\in\,\mathbb{Z}}\frac{k^{2}}{\left(4k^{2}-1\right)^{2}} = \frac{1}{2}\lim_{n\,\to\,\infty}\Im\oint_{C_n}\frac{z^{2}\cot\left(\pi z\right)}{\left(4z^{2}-1\right)^{2}}+\frac{\pi^2}{32}\,. $$

All that's left is to evaluate the limit of that contour integral and multiply both sides by $8$ to get the desired answer.

---

We construct a sequence of contour integrals $\displaystyle \oint_{C_n}f$ such that $\displaystyle \oint_{C_n}f$ converges as $n \to \infty$. As the contour grows bigger, none of the integer poles touch it because we judiciously constructed $C_n$ such that $\displaystyle \Re\left(n+\frac{1}{2}\right)e^{it}$ always lies in between two poles. A visual I made on Desmos can be found here and playing with the $n$ slider.

Letting $z \in C_n$, we use the parameterization $\displaystyle z = \left(n+\frac{1}{2}\right)e^{it}$ on $[0,2\pi]$. We bound the contour integral's modulus and have the following chain of inequalities below:

$$ \begin{align} 0 &\leq \left|\Im \oint_{C_n}f(z)dz\right| \\ &\leq \left|\oint_{C_n}f(z)dz\right| \\ &= \underbrace{\left|\operatorname{\Large\int_{0}^{2\pi}}\frac{\left(n+\frac{1}{2}\right)^{2}e^{2it}\cot\left(\pi\left(n+\frac{1}{2}\right)e^{it}\right)}{\left(4\left(n+\frac{1}{2}\right)^{2}e^{2it}-1\right)^{2}}\left(n+\frac{1}{2}\right)ie^{it}dt\right|}_{z \, \in\, C_n} \\ &\leq \operatorname{\Large\int_{0}^{2\pi}}\left|\frac{\left(n+\frac{1}{2}\right)^{2}e^{2it}\cot\left(\pi\left(n+\frac{1}{2}\right)e^{it}\right)}{\left(4\left(n+\frac{1}{2}\right)^{2}e^{2it}-1\right)^{2}}\left(n+\frac{1}{2}\right)ie^{it}\right|dt \\ &= \operatorname{\Large\int_{0}^{2\pi}}\frac{\left(n+\frac{1}{2}\right)^{3}\left|\cot\left(\pi\left(n+\frac{1}{2}\right)e^{it}\right)\right|}{\left|4\left(n+\frac{1}{2}\right)^{2}e^{2it}-1\right|^{2}}dt \\ &\leq \frac{\left(n+\frac{1}{2}\right)^{3}}{\left(4\left(n+\frac{1}{2}\right)^{2}-1\right)^{2}}\int_{0}^{2\pi}\left|\cot\left(\pi\left(n+\frac{1}{2}\right)e^{it}\right)\right|dt \\ &= \frac{\left(n+\frac{1}{2}\right)^{3}}{\left(4\left(n+\frac{1}{2}\right)^{2}-1\right)^{2}}\operatorname{\large\int_{0}^{2\pi}}\left|i+\frac{2i}{\exp\left(2\pi\left(n+\frac{1}{2}\right)ie^{it}\right)-1}\right|dt \\ &\leq \frac{\left(n+\frac{1}{2}\right)^{3}}{\left(4\left(n+\frac{1}{2}\right)^{2}-1\right)^{2}}\operatorname{\large\int_{0}^{2\pi}}\left(1+\frac{2}{\left|\exp\left(2\pi\left(n+\frac{1}{2}\right)ie^{it}\right)-1\right|}\right)dt \\ &\leq \frac{\left(n+\frac{1}{2}\right)^{3}}{\left(4\left(n+\frac{1}{2}\right)^{2}-1\right)^{2}}\operatorname{\large\int_{0}^{2\pi}}\mathop{\mathrm{sup}}_{t \in [0,2\pi]}\left(1+\frac{2}{\left|\exp\left(2\pi\left(n+\frac{1}{2}\right)ie^{it}\right)-1\right|}\right)dt \\ &= \frac{2\pi\left(n+\frac{1}{2}\right)^{3}}{\left(4\left(n+\frac{1}{2}\right)^{2}-1\right)^{2}}\mathop{\mathrm{sup}}_{t \in [0,2\pi]}\left(1+\frac{2}{\left|\exp\left(2\pi\left(n+\frac{1}{2}\right)ie^{it}\right)-1\right|}\right)\,. \end{align} $$

Here, we bound the integral by its supremum because the graph of $\displaystyle 1+\frac{2}{\left|\exp\left(2\pi\left(n+\frac{1}{2}\right)ie^{it}\right)-1\right|}$ is a square-looking wave for large $n$ periodic on $2\pi$.

Applying $n \to \infty$, we get

$$ \lim_{n \to \infty} 0 \leq \lim_{n\to\infty}\left|\Im \oint_{C_n}f(z)dz\right| \leq \frac{2\pi\left(n+\frac{1}{2}\right)^{3}}{\left(4\left(n+\frac{1}{2}\right)^{2}-1\right)^{2}}\mathop{\mathrm{sup}}_{t \in [0,2\pi]}\left(1+\frac{2}{\left|\exp\left(2\pi\left(n+\frac{1}{2}\right)ie^{it}\right)-1\right|}\right)\,. $$

Since the supremum is fixed and the numerator grows slower than the denominator, we can use the Squeeze Theorem for sequences to get

$$ \begin{align} &\lim_{n\to\infty}\left|\Im \oint_{C_n}f(z)dz\right| = 0 \\ \implies &\bbox[15px,#DBFFEA]{\lim_{n\to\infty}\Im \oint_{C_n}f(z)dz = 0\,.} \\ \end{align} $$

---

Wrapping things up,

$$ \require{cancel}{\sum_{k\,\in\,\mathbb{Z}}\frac{k^{2}}{\left(4k^{2}-1\right)^{2}} = \frac{1}{2}\cancelto{0}{\lim_{n\,\to\,\infty}\Im\oint_{C_n}\frac{z^{2}\cot\left(\pi z\right)}{\left(4z^{2}-1\right)^{2}}}+\frac{\pi^2}{32}\,.} $$

Then we just multiply both sides by $8$. Finally, we conclude that

$$ \bbox[15px,#E7FCFF,border:6px groove #51008C ]{\int_0^2 x \Biggl\lceil{\frac{1}{x}-\frac{1}{2}\Biggl\rceil}dx = \frac{\pi^2}{4}} $$

and we're finally done! $\blacksquare$

Happy New Year :)