In a triangle ABC : 2 externaly tangent circles, also tangent to BC with centers on line segments AB and AC : envelope of their lines of centers?

Question

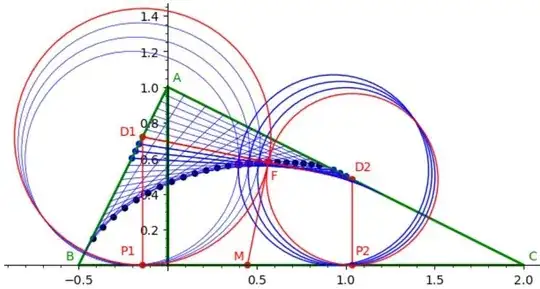
The figure here gives an illustration of the configuration described in the title in 4 cases ; consider especialy the fourth one, materialized by red circles, red center points, and a red line segment connecting them.

Fig. 1 : Circles on the left (resp. right) have their centers $D_1$ (resp. $D_2$) on $AB$ (resp. $AC$). Tangency points $F$ are represented by black dots (blue dots for our 4 cases).

I thought at first that the envelope of lines $D_1D_2$ coincides with the locus of the tangency points $F$ of the two circles, but this is not the case.

A particular remark : the radical axis of the two circles (the line orthogonal to the line of centers $D_1D_2$ in $F$) crosses $BC$ in a point $M$ which is the midpoint of the orthogonal projections $P_1,P_2$ of $D_1,D_2$ onto line $BC$. Moreover, I have established (analyticaly) that triangle $D_1MD_2$ is a right triangle in $M$.

My question : how can be described/obtained this envelope ? I have done a lot of analytical attempts but it looks very complicated in the general case. Maybe a more or less "pure geometry approach" is possible, but I don't see it... Same question for the arc of curve described by points $F$.

Remarks :

1. This question is a follow-on of this partial answer I had given to a recent question ; the latter shares many features with my present question, but asked in terms of a family of parabolas with common directrix $BC$ and focus $F$ ; the question there was also about an envelope, namely the envelope of circumscribed circles to $AD_1D_2$, supposed to be a circular arc.

2. As said above, I have done a lot of analytical calculations that can be followed in the SAGE program given below. In order to understand it, it suffices to say that :

• (WLOG) the coordinates of the vertices of triangle $ABC$ have been taken like this :

$$A(0,1), \ B(-1/a_1,0), \ C(-1/a_2,0).$$

• As a consequence, lines $AB$ and $AC$ have these resp. equations :

$$y=a_1 x +1, \ \ \ y=a_2 x +1$$

• As a consequence, the coordinates of $D_1$ and $D_2$ resp. are :

$$D_1(x_1,\underbrace{a_1x_1+1}_{y_1}), \ \ D_2(x_2,\underbrace{a_2x_2+1}_{y_2})$$

• The tangency conditions are summarized into the following relationship :

$$(P_1P_2)^2=4 P_1D_1 \times P_2D_2 \ \ \iff \ \ (x_1-x_2)^2=4(a_1x_1+1)(a_2x_2+1)$$

which isn't difficult to establish. This relationship, considered as a quadratic equation in $x_2$ when $x_1$ is considered as a parameter allows to take $x_1$ as the "driving parameter" : see the main "for-loop" in the SAGE program below where index $L$ is dirctly connected to $x_1$.

• The coordinates of point $F$ are :

$$F=(\frac{x_1y_2+x_2y_1}{y_1+y_2},\frac{2y_1y_2}{y_1+y_2})$$

SAGE program :

a1=2;a2=-1/2 # slopes of lines AB and AC resp.
g=line(((0,1),(-1/a1,0),(0,0),(0,1),(0,0),(-1/a2,0),(0,1)),color='green',thickness=2)
nu=25 # number of points
for L in range(2,nu) :
   x1=(L/nu-1)/a1;
   # x2 is the solution of quadratic equation (x1-x2)^2-4*(a1*x1+1)*(a2*x2+1)=0
   # or of -(x1-x2)^2+2*(a1*x1+1)^2+2*(a2*x2+1)^2-2*(a2*x2-a1*x1)^2=0
   b=x1+2*a1*a2*x1+2*a2
   c=x1^2-4*a1*x1-4
   x2=b+sqrt(b^2-c)
   y1=a1*x1+1;y2=a2*x2+1;
   c='blue';al=0.1;th=0.5
   g+=line(((x1,y1),(x2,y2)),color=c,alpha=1,thickness=th)
   m=1/(y1+y2)
   g+=point((m*(x1*y2+x2*y1),m*2*y1*y2),color='black',size=30) # point F
   if L in range(15,19) :
      g+=point((m*(x1*y2+x2*y1),m*2*y1*y2),color='red',size=50) # point F
      al=1;
      if L==18 :
         c='red'
         th=1
         g+=line((((x1+x2)/2,0),(m*(x1*y2+x2*y1),m*2*y1*y2)),color='red') # line FM
         g+=line(((x1,0),(x1,y1),(x2,y2),(x2,0)),color='red') # line P1-A1-A2-P2
         g+=point((x1,0),color='red',size=30) # point P1
         g+=point((x2,0),color='red',size=30) # point P2
         g+=point(((x1+x2)/2,0),color='red',size=30) # point M
      g+=circle((x1,y1),y1,color=c,alpha=al,thickness=th)
      g+=circle((x2,y2),y2,color=c,alpha=al)
      g+=line(((x1,y1),(x2,y2)),color=c,alpha=1)
      g+=point((x1,y1),color=c,size=30)
      g+=point((x2,y2),color=c,size=30)
show(g)

Answer 1

I'll use the same notation already introduced in the question: $$ =(0,1),\quad =\left(−{1\over _1},0\right),\quad =\left(−{1\over _2},0\right),\quad _1=(_1,1+_1_1). $$ From the equation given in the question we thus obtain $$ x_2=2 a_1 a_2 x_1+2 a_2+x_1 + \sqrt{(2 a_1 a_2 x_1 +2 a_2 + x_1)^2 +4 a_1 x_1-x_1^2+4}, $$ where $D_2=(x_2,1+a_2x_2)$, and from that the equations $f(x_1)=0$ of lines $D_1D_2$.

The envelope of the lines can be found by solving for $(x,y)$ the system formed by $f(x_1)=0$ and $f'(x_1)=0$. The result is too long to be written here, I'll just give the case $a_1=2$, $a_2=-1/2$ (as in the figure given in the question):

$$ x= \frac{10 + 30 x_1 + 25 x_1^2 + \sqrt{5 + 10 x_1} (-6 - 12 x_1 - 2 x_1^2)} {-5 x_1+\sqrt{10 x_1+5}-5} \\ \ \\ y= \frac{-20 - 40 x_1 + \sqrt{5 + 10 x_1} (8 + 12 x_1 - 3 x_1^2)} {2 \left(-5 x_1+\sqrt{10 x_1+5}-5\right)} $$ This is the parametric equation of the envelope (blue in figure below), as a function of parameter $x_1$.

The locus of $F$ can also be found (pink in figure below): $$ x_F= {2 \Delta + 2 (1 + a_1 \Delta) x_1 + a_1 x_1^2 + 2 a_2^2 x_1 (1 + a_1 x_1) + a_2 (2 + 4 a_1 x_1 + 2 \Delta x_1 + x_1^2 + 2 a_1^2 x_1^2) \over2 + a_1 x_1 + a_2 (2 \Delta + x_1) + 2 a_2^2 (1 + a_1 x_1)} \\ \ \\ y_F={2 (1 + a_1 x_1) (1 + a_2 (2 \Delta + x_1) + 2 a_2^2 (1 + a_1 x_1))\over2 + a_1 x_1 + a_2 (2 \Delta + x_1) + 2 a_2^2 (1 + a_1 x_1)} $$ where: $\Delta=\sqrt{(1 + a_1 x_1) (1 + a_2^2 + a_2 x_1 + a_1 a_2^2 x_1)}$.