Fixed tangent circle

Question

Consider fixed triangle ABC

Choose a point F inside ABC and consider the parabola with focus F and directrix BC. Let the intersection of the parabola with AB and AC be $D(F)$ and $E(F)$ respectively.

Let $\mathcal F$ be the set of $F$ such that $D(F),E(F),F$ are collinear.

Prove there is a circle $\omega$ such that for each $F\in \mathcal F$, the circle $\omega$ is tangent to the circumcircle of $A, D(F), E(F)$.

What I tried:

I tried several triangles and tried to find this circle, to no avail. Even the equilateral case is horrendous.

I also tried to use coordinates to characterize all possible F. You can WLOG parabola as y=x^2, then F = 1/4, BC is the line y=-1/4. Then you can let D be (a,a^2) and you get E is (-1/(4a), 1/(16a^2)). The coordinates of A are quite messy, and there doesn't seem to be a relation.

Can someone help with hints or solution?

Answer 1

Here is a figure drawn with Geogebra :

The (estimated) looked-for circular arc is dotted.

What follows is not an answer but a simplification of the issue :

Indeed, due to the focal/directrix definition of a parabola, the initial issue is equivalent to the configuration of two tangent circles with centers on $AB$ and $AC$ resp. which are tangent to $BC$ (see remark 1 below). Besides, the question remains the same : show that the circumcircle of $ADE$ is tangent to a fixed circular arc.

Why can we consider this approach as preferable ?

• because it replaces a more complex definition "Let $\mathcal{F}$ be the set of...". Instead, in the new setting, $F$ is plainly the point of tangency of the two circles.

• because, by eliminating the reference to the parabola and replacing it by tangent circles, more properties can be exploited.

Remarks :

1. A longer explanation for the genesis of the figure would be as follows. Being given a triangle $ABC$, let $D$ be a point on line segment $AB$. Let $(D)$ be the circle with center $D$ tangent to line $AB$. There is a unique circle $(E)$ with its center $E$ on line segment $AC$, tangent to $(D)$ and to line $AB$.

2. A classical property of a focal chord of a parabola is displayed on the figure : the tangents at the endpoints of the chord are orthogonal and they intersect on the directrix. Furthermore here, this point of intersection belongs to the common tangent to the two circles. See my answer here... 8 years ago...

3. See a follow-on of this question I have written where I am asking for a description of the envelope of line $DE$.

Answer 2

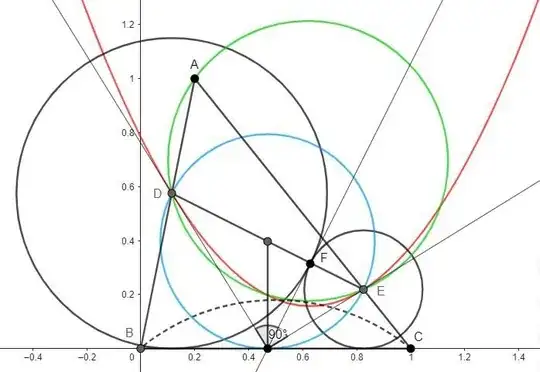
I rewrite my answer completely as I have found a synthetic proof.

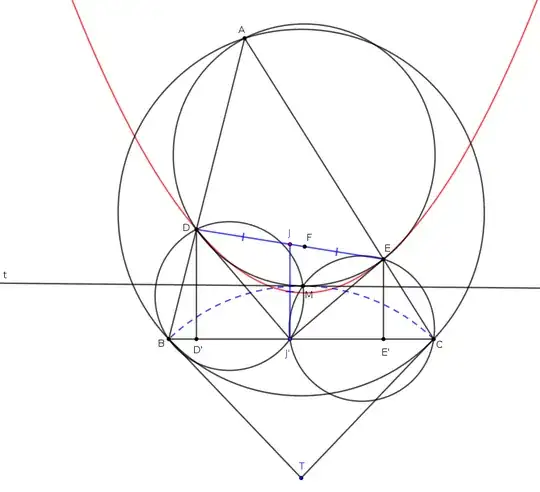
Proof. Let $J$ be the midpoint of $DE$. Let $D', J', E'$ be the orthogonal projections of $D, J, E$ onto $BC$.

$JJ'$ is the midline of the right trapezoid $DD'E'E$ so $JJ' = (DD' + EE')/2$. Because $DF = DD', EF = EE'$, it follows that $JJ' = (DF + EF)/2 = DE/2$. Therefore $DJ'E$ is a right triangle where $\angle DJ'E = \frac{\pi}{2}$.

Apply Miquel's theorem to triangle $ABC$ and three points $J', E, D$, we obtain that the circumcircles of triangles $ADE, BDJ', CEJ'$ have a common point. Denote this common point by $M$.

If $\angle BAC = \frac{\pi}{2}$ then the circumcircle of triangle $ADE$ is also the circle with diameter $DE$, tangent to $BC$ at $J'$. In this case, $BC$ is the fixed tangent circle, but it degenerates into a straight line.

Otherwise, $\angle BAC \ne \frac{\pi}{2}$. Chasing oriented angles $$ \begin{align*} (MB, MC) & \equiv (MB, MJ') + (MJ', MC) \\ & \equiv (DB, DJ') + (EJ', EC) \\ & \text{($D, B, M, J'$ are concyclic; $E, C, M, J'$ are concyclic)} \\ & \equiv (DB, EC) + (EJ', DJ') \\ & \equiv (AB, AC) + \frac{\pi}{2} \pmod{\pi} \end{align*} $$

$(AB, AC) + \frac{\pi}{2} \pmod{\pi}$ is fixed so $M$ lies on a fixed circle (using the inscribed angle theorem, one can show that the center of this fixed circle is $T$, where $TB, TC$ are tangent to the circumcircle of triangle $ABC$).

It remains to show that the circumcircles of triangles $ADE$ and $MBC$ are tangent. Let $t, t'$ be the tangent line at $M$ of the circumcircles of triangles $ADE, MBC$, correspondingly. Chasing oriented angles, using tangent-chord theorem and concyclic points $$ \begin{align*} (t, MB) & \equiv (MM, MD) + (MD, MB) \\ & \equiv (EM, ED) + (J'D, J'B) \\ & \equiv (EM, EJ') + (EJ', ED) + (J'D, J'B) \\ & \equiv (CM, CJ') + (EJ', ED) + (J'E, J'J) & (J'D\perp J'E, J'B \perp J'J) \\ & \equiv (CM, CB) + \underbrace{(EJ', EJ) + (J'E, J'J)}_{\equiv 0} & \text{($JJ'E$ is isosceles)} \\ & \equiv (CM, CB) \\ & \equiv (t', MB) \pmod{\pi} \end{align*} $$

Therefore $t$ is identical to $t'$, which means the circumcircles of triangles $ADE$ and $MBC$ are tangent to each other. Hence the circumcircle of triangle $ADE$ is tangent to a fixed circle (or straight line). Q.E.D.