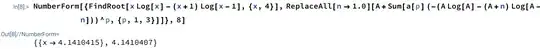Is $x^x = (x-1)^{x+1}$?

Question

Background: I was trying to estimate the size of $21^{21}$ for some problem and decided to use $20^{22}$ as hopefully a rough approximate ($20^{22} = 2^{22} \cdot 10^{22} \approx 10^{28}$). But then I wanted to see if that was over or underestimate and got into this rabbithole of when they are equal.

Anyways, I was doing some thinking and wanted to get an analytical solution to when $x^x = (x-1)^{x+1}$. My original question was which was bigger for $x=21$, but transitioned when I noticed that the $x^x > (x-1)^{x+1}$ for small $x$, and then it flips when I go from $x=4$ to $x=5$. I threw it in Desmos and got an approximate value of 4.141 (and I went woahhh that's $\pi +1$ but unfortunately that's only true to a couple decimal places :( ). Can anyone help me find an analytical or algebraic (as opposed to numerical/approximate) way of finding the value for x when these two expressions are equal?

I was trying to approach it in a similar way to when $a^b$ grows faster than $b^a$ using logarithms but was struggling and would love some help if anyone has any suggestions. There is also this post which is similar but only talks about the inequality whereas I am more concerned about the equality.

EDIT

I found this paper which connects the $x$ value of the solution to the original equation to be equal to $\alpha_0$ where $1+\frac{1}{(1+\frac{1}{(1+\frac{1}{...})^{\alpha}})^{\alpha}}$ converges for all $0 < \alpha < \alpha_0$ and diverges for all $\alpha > \alpha_0$. Very interesting stuff.

PS: I have an interesting follow up for $x^x$ vs $(x-n)^{x+n}$ that I would like to ask about but maybe some insight on this question will allow me to explore the following on my own :) Thanks!

Answer 1

Consider the function $$f(x)=x^x - (x-1)^{x+1}$$ $$f'(x)=-\frac{2}{x-1}+\log \left(\frac{x}{x-1}\right)$$ cancels around $x=3.70965$ (this is just a number. Lambert function is of no use here) and the second derivative test confirms that this is a maximum.

Now, as you noticed, $f(x)=0$ happens for $x=4.14104$ which is just another number.

If you want to explore $$f_n(x)=x^x-(x-n)^{x+n}$$ this is an interesting problem. I let you the pleasure of making the conjecture that the zero of $f_n(x)$ is something like $$x_{\text{sol}} \sim a+b\,n $$ Adjust the constants $(a,b)$ using linear regression.

By the way, there is one $n$ such that $x_{\text{sol}}$ is an integer (I only know one). Find it.

Edit

If you look for a fast numerical method, consider the function $$g(x)=x\log(x)-(x+n)\log(x-n)$$ Using $x_0=(n+3)$ (the $3$ is not random at all), the first iterate of Newton method is $$x_1=\frac{n (2 n+6-3 \log (3))}{2 n-3 \log(n+3)+3 \log (3)}$$ which gives $x_1=4.13751$ for $n=1$ and $x_1=7.84460$ for $n=4$.

Since $f(x_1)>0$ and $f''(x_1)>0$, by Darboux theorem, we already know that $x_1$ is an underestimate of the solution.

You could do better using the first iterate of Halley or Householder methods but the formulae are quite messy. For the two above examples, Halley method gives $x_1=4.14107$ and $x_1=8.00801$.

If you continue with this problem, you can work a much better approximation than the miserable linear one I suggested in my answer.

Update $1$

For the base case where $n=1$, using (as proposed above) $$x_0=\frac {8-3\log(3)}{2+3\log(3)-6\log(2) }$$ computing the first iterate of a Newton-like method of order $k$, we have a (messy) fully expression for $x_1^{(k)$.

The table below reports the value of the absolute error as a function of the order $k$

$$\left( \begin{array}{cc} k & \Delta_k & \text{method}\\ 2 & 2.17247\times 10^{-6} &\text{Newton}\\ 3 & 4.08878\times 10^{-10} &\text{Halley}\\ 4 & 2.29023\times 10^{-13} &\text{Householder}\\ 5 & 1.61198\times 10^{-16} &\text{no name}\\ 6 & 1.26797\times 10^{-19} &\text{no name}\\ \end{array} \right)$$

that is to say $$\Delta_k \sim \,e^{1.55(1-5k) }$$

Update $2$

Using

$$x_0=\frac{n (2 (n+a)-a \log (a))}{2n-a \log (n+a)+a \log (a)}$$ it seems that a good approximation of the solution is simply given by $$a \sim 2+\sqrt n$$ and we still know by Darboux theorem that this is an underestimate of the solution.

Answer 2

This equation has many variables, so methods like Lagrange inversion or transforms would be hard to apply. However, series reversion works well. First, use @Claude Leibovici’s answer to notice that $x\sim a=n+\sqrt n+2$, set $x=v+a$ and subtract $v_0$ so it contains $(0,0)$:

$$x^x=(x-n)^{x+n}\iff f(v)=(v+a)\ln(v+a)-(v+a+n)\ln(v+a-n)-v_0=-v_0,v_0= a\ln(a)-(a+n)\ln(a-n)$$

with $f^{-1}(v)=y(v)$. We use a power series method. Firstly, find a differential equation for $y$:

$\frac1{y’}=\ln(y+a)-\ln(y+a-n)-\frac{2n}{y+a-n}\iff -a(a-n)^2y’’= (a-n)(3a-n)yy’’ +n(a+n)y’^3+ (3a-2n)y^2y’’ +nyy’^3+y^3y’’,y(0)=0,y’(0)=\frac{a-n}{(a-n)(\ln(a)-\ln(a-n))-2n}$

Substituting $y=\sum\limits_{p=1}^\infty a_pv^p$:

$$-a(a-n)^2\sum_{p=1}^\infty a_pp(p-1)v^{p-2}=(a-n)(3a-n)\sum_{m=1}^\infty\sum_{k=1}^\infty a_ma_k k(k-1) v^{m+k-2}+n(a+n) \sum_{m=1}^\infty\sum_{k=1}^\infty\sum_{j=1}^\infty a_ma_ka_jmkj v^{m+k+j-3}+(3a-2n) \sum_{m=1}^\infty\sum_{k=1}^\infty\sum_{j=1}^\infty a_ma_ka_jj(j-1)v^{m+k+j-2}+n \sum_{m=1}^\infty\sum_{k=1}^\infty\sum_{j=1}^\infty\sum_{r=1}^\infty a_ma_ka_ja_rmkjv^{m+k+j+r-3}+ \sum_{m=1}^\infty\sum_{k=1}^\infty\sum_{j=1}^\infty\sum_{r=1}^\infty a_ma_ka_ja_r r (r-1) v^{m+k+j+r-2}$$

Gathering powers of $v$, index shifting, and combining sums gives a recurrence relation for the coefficients. We can use it to invert $f(v)=(v+a)\ln(v+a)-(v+a+n)\ln(v+a-n)-v_0$ or $x^x(x-n)^{-x-n}=b$ equivalently. However, the solution to the question’s equation is at $x=a+y(-v_0)$, so we set $v=-v_0$ and therefore:

$$\begin{aligned}\bbox[2px,border:3px solid blue]{x^x=(x-n)^{x+n}\iff x=a+\sum_{p=1}^\infty a_p((a+n)\ln(a-n)-a\ln(a))^p\\-a p(p-1) (a-n)^2 a_p=\sum_{m=1}^{p-1}ma_m a_{p-m} (a_1 n (a+n)(p-m)+(m-1)(a-n)(3a-n))+\sum_{m=1}^{p-1}\sum_{k=1}^{p-m-1}a_ma_{p-m-k}(k(k-1)(3a-2n)a_k+mn(a+n)(k+1)(p-m-k)a_{k+1})+\sum_{m=1}^{p-1}\sum_{k=1}^{p-m-1}\sum_{j=1}^{p-m-k}ja_ma_ka_j(nmk a_{p-m-k-j+1}+(j-1)a_{p-m-k-j})\\a_p=\left\{\frac{a-n}{(a-n)(\ln(a)-\ln(a-n))-2n},-\frac{n(a-n)(a+n)}{2a((a-n)(\ln(a)-\ln(a-n))-2n)^3},\frac{n(a-n)((2a^3+a^2n-4an+n^3)(\ln(a)-\ln(a-n)) -a^2n+5n^3)}{6a^2 ((a-n)(\ln(a)-\ln(a-n))-2n)^5} ,\dots\right\}}\end{aligned}$$

There is a pattern: $a_p=\frac{N_p}{p!a^{p-1}(((a-n)(\ln(a)-\ln(a-n))-2n)^{2p-1}}$ where $N_p=n(a-n)(\cdots),p>1$

Interestingly, $a_p=0$ if $n=4$ as then $x=a=8$ is the solution. Redefining a better initial $a$ will make the series converge more quickly. Using 1/(-A (A-n)^2 p (p-1))( Sum[a[p-m]a[m]m((2 A (A-n)+(A-n)^2)(m-1) +n (A+n) a[1] (p-m)),{m,1,p-1}]+Sum[Sum[a[m] a[p-m-k](n (A+n) a[k+1] m(k+1) (p-m-k)+(A+2 (A-n)) a[k] (k) (k-1)),{k,1,p-m-1}],{m,1,p-1}]+ Sum[Sum[Sum[a[m] a[k] a[j]j( a[p-m-k-j+1] n m k+ a[p-m-k-j] (j-1)),{j,1,p-m-k}],{k,1,p-m-1}],{m,1,p-1}]) and A+Sum[a[p] (-(A Log[A]-(A+n)Log[A-n]))^p,{p,1,P}] for given P and A$=a$ shows 3 terms of the series give 6 to 7 correct decimal places:

Answer 3

The ratio $(x-1)^{x+1}\over x^x$ is eay to estimate $\rho = (x-1).(1-{1\over x})^x=(x-1) e^{x \log(1-{1\over x})}$ Now $x \log(1-{1\over x})=-1-1/2{1\over x}+o({1\over x})$

So $\rho= (x-1)e^{-1} (1-1/2{1\over x}+o({1\over x}))=e^{-1}(x-3/2+o(1))$

It is not very difficult to rpove that the $o(1/x)$ in the forts line is $<1/800$ for $x>20$, so in your case the ratio is about $e^{-1}(21-3/2)>>1$

Answer 4

For the case where $n=1$, using @TravisWillse's approach (have a look here, we have $$x\sim e+\frac{3}{2}-\frac{7}{24 e}+\frac{1}{3 e^2}-\frac{911}{1920 e^3}+\frac{34}{45 e^4}-\frac{748075}{580608 e^5}+\frac{1933}{840 e^6}-\frac{845935879}{199065600 e^7}+\frac{342242}{42525 e^8}-\frac{23534545109}{1513881600 e^9}+\frac{219211733}{7185024 e^{10}}-\frac{132923977533492797}{2191186722816000 e^{11}}+\frac{3844997129}{31531500 e^{12}}-\frac{11008825409688168233}{4449794575 5648000 e^{13}}+\frac{182282337018689}{360277632000e^{14}}+\cdots$$ which, converted to decimals is $\color{red}{4.141}22$ but we could continue.