Recently, a post addressed the classic interesting question of showing that the projection onto a closed convex part of $\mathbb R^2$ is contracting. Unfortunately, the person did not provide any trace of personal research. Nevertheless, the question interested me and I wanted to find old posts that dealt with it. I found a very interesting post with figures and a real effort to make things clear and meaningful.
But there are two points that bother me in the post in question.
First, I corrected typos that did not seem to have been noticed despite the many readings of this post.
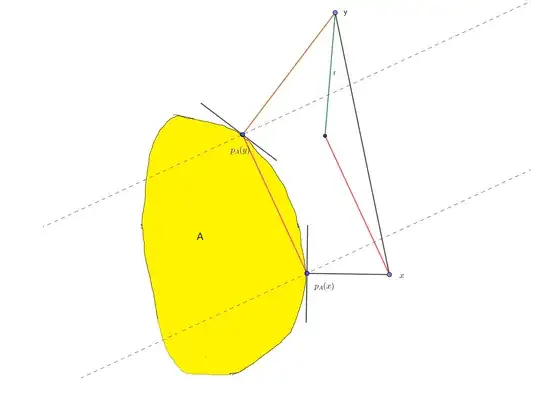
Let $A$ a convex of $\mathbb R^2, x,y \in \mathbb R^2, p_A(x) $ and $p_A(y) $ their projections on $A$, $v= p_A(y)-p_A(x)$. It is not proven that the segment $[x,y]$ crosses the two lines orthogonal to $v$ and passing through $p_A(x)$ and $p_A(y)$.
So I am trying to prove it. I've already proven that $$\boxed{\forall z\in A, \langle z-p_A(x),x-p_A(x)\rangle\le 0}\color{red}{(*)}$$ by following Schneider's hints.
Similarly I obtained that$$\forall z\in A, \langle z-p_A(y) ,y-p_A(y) \rangle \le 0$$
I know that the line orthogonal to $v$ and passing through $p_A(x)$ $$\{\xi\in\mathbb R^2: \langle \xi-p_A(x) ,v \rangle=0\}$$divides $\mathbb R^2 $ into two half-planes $$\boxed{\{\xi\in\mathbb R^2: \langle \xi-p_A(x) ,v \rangle\le 0\}}\color{green}{(**)}$$ and $$\{\xi\in\mathbb R^2: \langle \xi-p_A(x) ,v \rangle\ge 0\}$$
I see that I can replace $z$ by $p_A(y)$ in $\color{red}{(*)}$ and $\xi$ by $x$ in $\color{green}{(**)}$ to place $x$ in one of the half-planes.
But afterwards, I admit that it becomes a headache for me to finish the demonstration expected by Schneider all by myself. I hope this very specific question is not a dupe and that it will deserve your attention so that we really finish this demonstration of an important fact if it has not already been done on MSE.