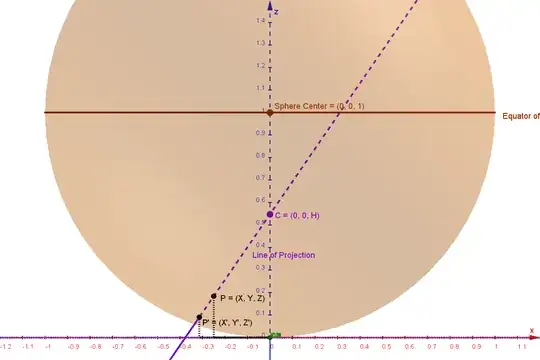
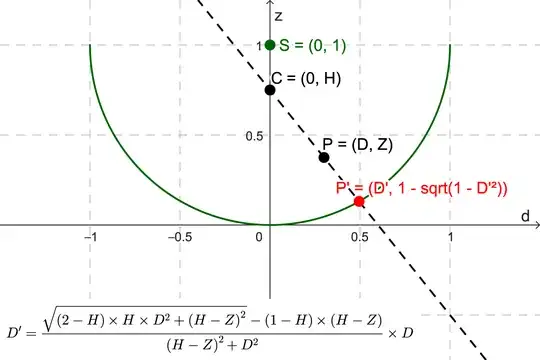
For a sphere with centre $\mathbf{a}$ and radius $r$, the equation of the sphere is $ || \mathbf{x} - \mathbf{a} ||^2 = r^2$, and since we are projecting onto a point $P'$ that lies on the sphere, this equation holds for $\mathbf{x} = \mathbf{p}'$. On the other hand, $P'$ must lie on the line between the centre of projection $C$ and the point you are projecting $P$, so $\mathbf{p'} = \mathbf{c} + t(\mathbf{p}-\mathbf{c})$ which you may prefer to think of the linear combination $\mathbf{p'} = (1-t)\mathbf{c} + t\mathbf{p}$. When the parameter $t=0$ we are at the centre of projection $C$, when $t=1$ we are at point $P$, and if we keep moving further in that direction then $t>1$. Putting these facts together, you need to solve the quadratic equation
$$||t(\mathbf{p} - \mathbf{c}) + \mathbf{c} - \mathbf{a}||^2 = r^2$$
for $t$. Doing so will give you two values for $t$, so the problem is which value of $t$ to pick. I don't actually know the convention for projection onto a sphere (unlike a plane, the line joining the point you want to project and the centre of projection can intersect twice with the sphere you want to project onto, so which one is "the" projection?) and I have posted a Math SE question, as yet unanswered, asking precisely this point. But you seem to have a practical situation in mind, so you should use that to inform which $t$ is appropriate for your needs.
I have oriented the equation of the line so that the parameter $t$ increases as you move from the centre of projection, $\mathbf{c}$ (where $t=0$), to the point you want to project, $\mathbf{p}$ (where $t=1$). So if your application requires you to treat $\mathbf{c}$ as if it were a light source, and "cast a shadow" of $\mathbf{p}$ onto the sphere, then you reach $\mathbf{p'}$ by continuing along the line in the direction of increasing $t$, so you just need to pick the larger of your two $t$ solutions: so long as $P$ is inside the sphere, then $t$ will be a positive number greater than one. (The line will hit the sphere again at the point where $C$ casts a shadow on the sphere if you treat $P$ as a light source, but that's going "backwards" so has a negative $t$.)
If I understood correctly, you want $r=1$, the centre of the sphere at $\mathbf{a} = (0, 0, 1)^t$ and centre of projection at $\mathbf{c} = (0, 0, H)^t$ so $\mathbf{c} - \mathbf{a} = (0, 0, H-1)^t$ and the squared distance between the two centres is $||\mathbf{c} - \mathbf{a}||^2 = (H-1)^2$. Similarly the squared distance between the point $P$ and the centre of projection is $||\mathbf{p} - \mathbf{c}||^2 = X^2 + Y^2 + (Z-H)^2$. Finally, we note that the scalar product of $\mathbf{c} - \mathbf{a}$ with $\mathbf{p} - \mathbf{c}$ is $(0, 0, H-1)^t \cdot (X, Y, Z-H) = (H-1)(Z-H)$. If we expand our equation for $t$ so we can more easily see the quadratic coefficients:
\begin{align}
\left( t(\mathbf{p} - \mathbf{c}) + \mathbf{c} - \mathbf{a} \right) \cdot \left( t(\mathbf{p} - \mathbf{c}) + \mathbf{c} - \mathbf{a} \right) &= r^2 \\
\implies ||\mathbf{p} - \mathbf{c}||^2 t^2 + 2(\mathbf{c} - \mathbf{a}) \cdot (\mathbf{p} - \mathbf{c}) t + ||\mathbf{c} - \mathbf{a}||^2 - r^2 &= 0 \\
\implies (X^2 + Y^2 + (Z-H)^2)t^2 + 2(H-1)(Z-H)t + (H-1)^2 - 1 &= 0
\end{align}
These coefficients can then be substituted into the quadratic formula $t = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$. It comes out slightly nicer if we notice the constant term is $H^2 - 2H = H(H-2)$ and we divide the quadratic equation by two because of the factor of two in front of the $t$ term:
\begin{align}
t &= \frac{-(H-1)(Z-H) \pm \sqrt{(H-1)^2(Z-H)^2 - H(H-2)(X^2 + Y^2 + (Z-H)^2)}}{X^2 + Y^2 + (Z-H)^2} \\
\implies t &= \frac{(1-H)(Z-H) \pm \sqrt{(Z-H)^2 - H(H-2)(X^2 + Y^2)}}{X^2 + Y^2 + (Z-H)^2} \\
\implies t &= \frac{\pm \sqrt{H(2-H)(X^2 + Y^2) + (Z-H)^2} - (1-H)(H-Z)}{X^2 + Y^2 + (Z-H)^2}
\end{align}
where I've tried rearranging to make it look more like your result. If I understand your practical objective correctly, you want the positive square root so that $t$ corresponds to the point on the sphere you reach if you move in the direction from $C$ to $P$. Finally, once you solved numerically for $t$, you can find the coordinates of $P'$ by substituting into $\mathbf{p'} = \mathbf{c} + t(\mathbf{p}-\mathbf{c})$:
\begin{align}
(X', Y', Z') = (0, 0, H)^t + t(X, Y, Z - H)^t \\
\implies \begin{cases} X' &= Xt \\ Y' &= Yt \\ Z' &= (Z - H)t + H
\end{cases}
\end{align}
If you were doing for this for many points $P$, but wanted to keep the centre of projection $C$ and centre $A$ and radius $r$ of the sphere fixed, then you could:
- pre-compute and store $\mathbf{c} - \mathbf{a}$ and $||\mathbf{c} - \mathbf{a}||^2 - r^2$ so they don't need to be recalculated for each point $P$,
- for each $P$, find $\mathbf{p} - \mathbf{c}$ and hence $||\mathbf{p} - \mathbf{c}||^2$ and $(\mathbf{c} - \mathbf{a}) \cdot (\mathbf{p} - \mathbf{c})$,
- solve $||\mathbf{p} - \mathbf{c}||^2 t^2 + 2(\mathbf{c} - \mathbf{a}) \cdot (\mathbf{p} - \mathbf{c}) t + ||\mathbf{c} - \mathbf{a}||^2 - r^2 = 0$ for $t$, and for your application taking the larger, positive root (you might not want to do this by the conventional quadratic formula, see here, here and here),
- substitute your $t$ into $X' = Xt$, $Y' = Y$ and $Z' = (Z - H)t + H$.
This should be substantially faster than using big nasty formulas for $X'$, $Y'$ and $Z'$ separately — the gnarly bit really only needs to be computed once per point $P$, and some parts don't need to be recomputed at all if $A$, $C$ and $r$ are fixed.