Question Summary
I have a triangular patch of a sphere, and I want to triangulate it by arranging vertices on the surface as evenly as possible using points whose 3D coordinates are given by three functions of two parameters $(X(u, v), Y(u, v), Z(u, v))$. Specifically, I want to find three functions such that:
- the difference in the lengths of the shortest and longest segments joining neighboring vertices is as small as possible,
- one vertex is located exactly in the center of the patch, at $(0, 0, 0)$,
- the arrangement of vertices has three-fold rotational symmetry about the $z$-axis and reflection symmetry about the $yz$-plane, and
- the three functions which give the coordinates of the vertices are continuous over the entire domain of both parameters.
UPDATE on Second Attempt
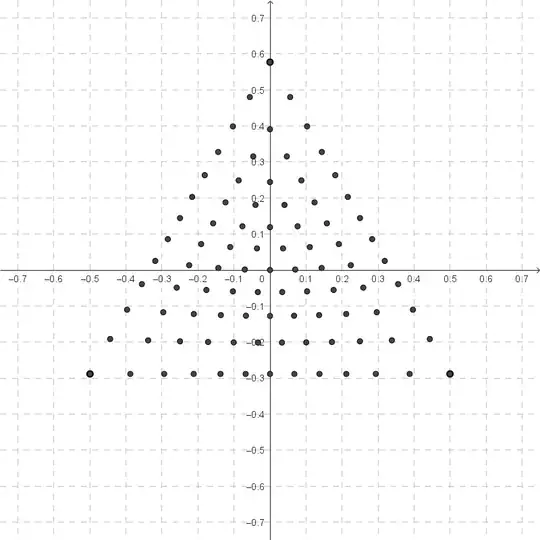
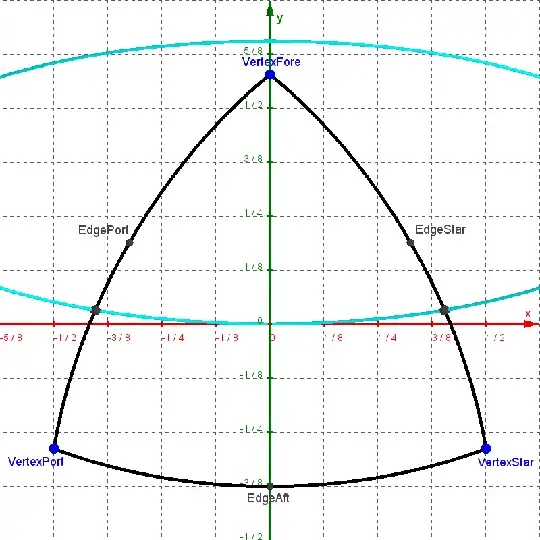
I took the points that I generated with rotations on the surface of the sphere (see "My Second Attempt" section below) and projected them onto the $xy$-plane:
Logically, if I can algebraically create a grid of points in an arrangement that mimics this geometrically-created one, I can use the projection equations from my first attempt to map the algebraic grid back onto the sphere. However, I haven't been able to find a set of equations that mimics this arrangement.
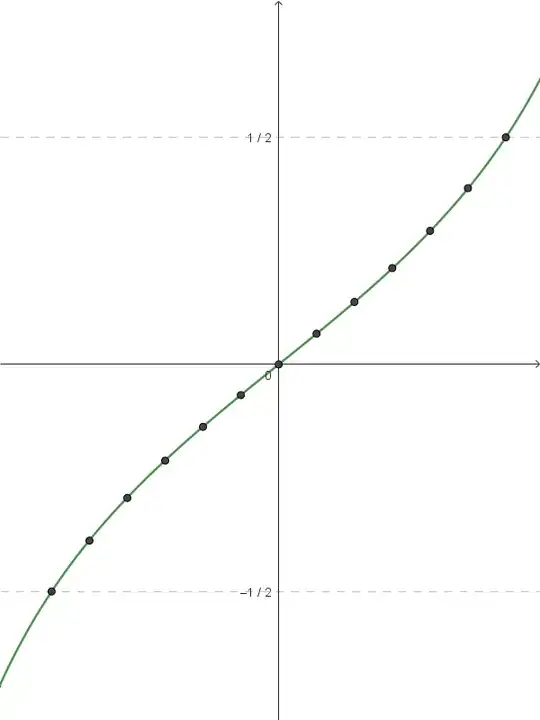
As a start, I took the points in the bottom row and plotted each one's actual $x$-coordinate against the rotation that generated the point it is a projection of, normalized to the interval $\left[-\frac{1}{2}, \frac{1}{2}\right]$:
The points seem to be tracing out a shape very similar to the tangent function. A little playing-around-with-variables showed that the points are extremely close to the function $\frac{1}{2} \cot\left(\frac{3}{4}\right) \tan\left(\frac{3}{2} x\right)$:
I can easily use that function to approximate the bottom row of projected points. However, I haven't been able to find a way to translate this small success into the higher rows of projected points. Does anyone know how to do that?
UPDATE TWO on Second Attempt
I worked out that the pair of equations
$$ X(u, v) = \frac{\cot\left(\frac{3}{4}\right)}{2} \left(\tan\left(\frac{3}{2} \left(u - \frac{1}{2}\right)\right) + \frac{\tan\left(\frac{3}{2} \left(v - \frac{1}{2}\right)\right)}{2}\right) + \frac{1}{4} $$ $$ Y(v) = \frac{\sqrt{3}}{2} \left(\frac{\cot\left(\frac{3}{4}\right)}{2} \tan\left(\frac{3}{2} \left(v - \frac{1}{2}\right)\right) + \frac{1}{6}\right) $$
lines up quite nicely with the projected points on all three edges of the triangle for $0 ≤ u ≤ 1$ and $0 ≤ v ≤ u$, but fails to line up with any points on the interior of the triangle. I'm now attempting to find a way to nudge the interior equation-points towards the projection-points without breaking the alignment of the edge equation-points and projection-points. It seems likely that $Y(v)$ will need to become $Y(u, v)$, but how to go about that is so far eluding me.
The Setup
Start with a sphere of radius $1$ centered on the point $(0, 0, 1)$. Consider only the triangular section of the sphere bounded by three circular arcs which lie on the surface of the sphere, each defined by passing through three out of six points. The six points are:
- $VertexFore = \left(0, \frac{\sqrt{3}}{3}, 1 − \frac{\sqrt{6}}{3}\right)$
- $EdgeStar = \left(\frac{4 + 5 \sqrt{2}}{34}, \frac{4 + 5 \sqrt{2}}{34 \sqrt{3}}, 1 − \frac{20 \sqrt{2} - 1}{17 \sqrt{3}}\right)$
- $VertexStar = \left(\frac{1}{2}, −\frac{\sqrt{3}}{6}, 1 − \frac{\sqrt{6}}{3}\right)$
- $EdgeAft = \left(0, −\frac{4 + 5 \sqrt{2}}{17 \sqrt{3}}, 1 − \frac{20 \sqrt{2} - 1}{17 \sqrt{3}}\right)$
- $VertexPort = \left(−\frac{1}{2}, −\frac{\sqrt{3}}{6}, 1 − \frac{\sqrt{6}}{3}\right)$
- $EdgePort = \left(−\frac{4 + 5 \sqrt{2}}{34}, \frac{4 + 5 \sqrt{2}}{34 \sqrt{3}}, 1 − \frac{20 \sqrt{2} - 1}{17 \sqrt{3}}\right)$
And the three circular arcs are:
- $arcPort$, passing through $VertexPort$, $EdgePort$, and $VertexFore$
- $arcStar$, passing through $VertexStar$, $EdgeStar$, and $VertexFore$
- $arcAft$, passing through $VertexPort$, $EdgeAft$, and $VertexStar$
I know that the triangles can't all be exactly the same size because equal-sized triangles naturally tile a flat plane, not a curved surface, so some distortion is necessary to make them fit. It also seems like the fact that the boundaries of the patch of sphere I'm concerned with aren't great circles increases the required amount of distortion. With that in mind, I just want to minimize the distortion as much as possible.
My First Attempt
The three planes in which the boundary-arcs lie intersect at a single point, $C = \left(0, 0, 1 + \frac{\sqrt{3} − \sqrt{24}}{7}\right)$. If we place a triangular grid of points at the same height as the three corner points with coordinates $\left(u + \frac{v − 1}{2}, \frac{\sqrt{3}}{2} \left(v − \frac{1}{3}\right), 1 − \frac{\sqrt{6}}{3}\right)$ and with $0 ≤ u ≤ 1$ and $0 ≤ v ≤ 1 − u$, we can project them all from point $C$ onto the surface of the sphere with parametric coordinates
$$ X(u, v) = \left(u + \frac{v − 1}{2}\right) \frac{\frac{3 + \sqrt{2}}{7} \sqrt{2 (u^2 + u v + v^2 − u − v) + 1} − \frac{1 + 5 \sqrt{2}}{49}}{u^2 + u v + v^2 − u − v + \frac{20 + 2 \sqrt{2}}{49}} $$
$$ Y(u, v) = \frac{\sqrt{3}}{2} \left(v − \frac{1}{3}\right) \frac{\frac{3 + \sqrt{2}}{7} \sqrt{2 (u^2 + u v + v^2 − u − v) + 1} − \frac{1 + 5 \sqrt{2}}{49}}{u^2 + u v + v^2 − u − v + \frac{20 + 2 \sqrt{2}}{49}} $$
$$ Z(u, v) = 1 − \sqrt{1 − \left(\sqrt{u^2 + u v + v^2 − u − v + \frac{1}{3}} × \frac{\frac{3 + \sqrt{2}}{7} \sqrt{2 (u^2 + u v + v^2 − u − v) + 1} − \frac{1 + 5 \sqrt{2}}{49}}{u^2 + u v + v^2 − u − v + \frac{20 + 2 \sqrt{2}}{49}}\right)^2} $$
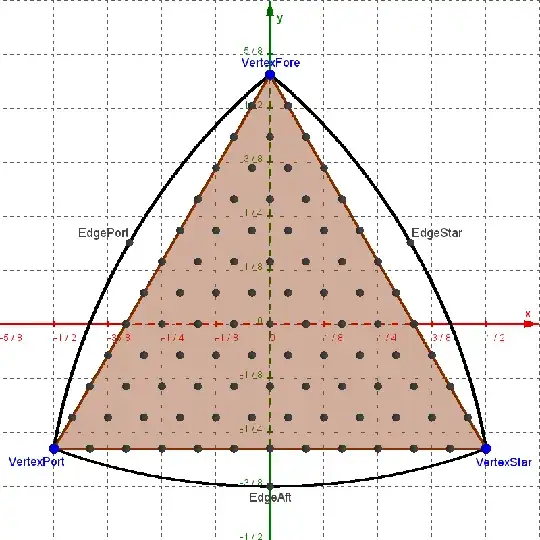
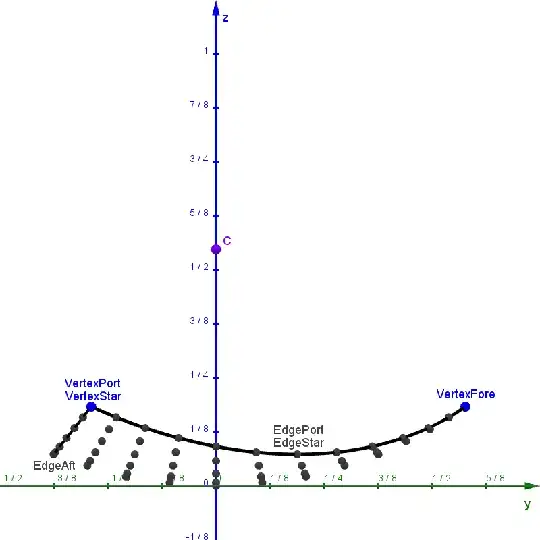
To get a point at $(0, 0, 0)$ with evenly-sized steps, the steps taken in both $u$ and $v$ need to be of the form $\frac{1}{3 n}$, where $n$ is a positive integer number of subdivisions. For $n = 4$ as an example, we get the following grid of starting points:
And the projected points from the $(X, Y, Z)$ expressions:
While this method of creating points is straightforward and symmetrical, it is not very even. The points are bunched up in the corners of the triangular patch and spread out in the center, and the longest line segment of the triangulation is almost twice the length of the shortest line segment. I want to do better.
My Second Attempt
The bounding-curve $arcAft$ is a portion of a larger circle which lies on the surface of the sphere. I calculated its center-point to be $P = \left(0, −\frac{2 \sqrt{3} − 6 \sqrt{6}}{51}, 1 + \frac{9 \sqrt{3} − 10 \sqrt{6}}{51}\right)$. The arc-endpoints $VertexStar$ and $VertexPort$ span an angle of $α = \arccos\left(\frac{\sqrt{8} − 1}{4}\right)$. I can rotate $VertexPort$ about $P$ by an angle $u × α$ with $0 ≤ u ≤ 1$ to get the point
$$ $$ \begin{pmatrix} −\frac{1}{2} \cos(u × α) + \sqrt{\frac{23 + 16 \sqrt{2}}{68}} \sin(u × α), \\ \frac{6 \sqrt{6} − 2 \sqrt{3}}{51} − \sqrt{\frac{457 + 312 \sqrt{2}}{3468}} \cos(u × α) − \sqrt{\frac{527 − 136 \sqrt{2}}{3468}} \sin(u × α), \\ 1 + \frac{9 \sqrt{3} − 10 \sqrt{6}}{51} − \sqrt{\frac{716 + 504 \sqrt{2}}{3468}} \cos(u × α) − \sqrt{\frac{5 + 2 \sqrt{2}}{51}} \sin(u × α) \end{pmatrix} $$ $$
Unfortunately, the factor of $u$ means that $\cos\left(u × \arccos\left(\frac{\sqrt{8} − 1}{4}\right)\right)$ and $\sin\left(u × \arccos\left(\frac{\sqrt{8} − 1}{4}\right)\right)$ don't reduce at all except for the specific cases of $u = 0$ (the start-point $VertexPort$, already known), $u = \frac{1}{2}$ (the mid-point $EdgeAft$, already known), and $u = 1$ (the end-point $VertexStar$, already known). All other $u$-values seem to be stuck with the awkward nested regular-and-inverse-trig-function unpleasantness. But let's persevere and see if it gets nicer later on.
Again because of the requirement to have a point at the exact center, the points one-third and two-thirds of the way along the arc are significant. We can use the above formula for a point plus rotation about the $z$-axis to find the aft-third points on $arcPort$ and $arcStar$, and then we can find the center of the circle $cThird$ which passes through both those points and the center-point of the patch $(0, 0, 0)$. Unfortunately, the algebra for that seems to be an irreducible nightmare, but for now lets ignore the algebra and continue to persevere geometrically.
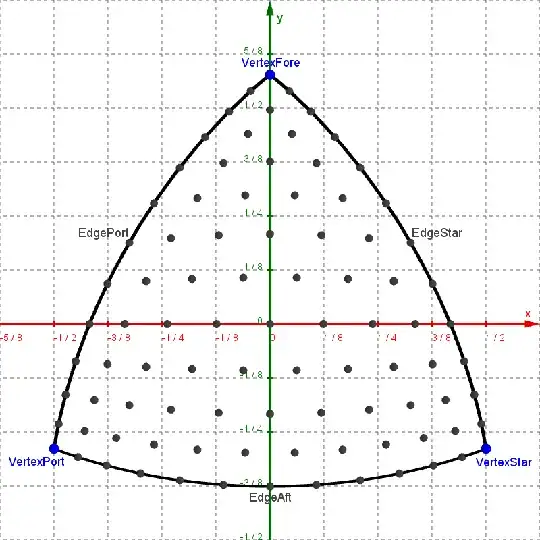
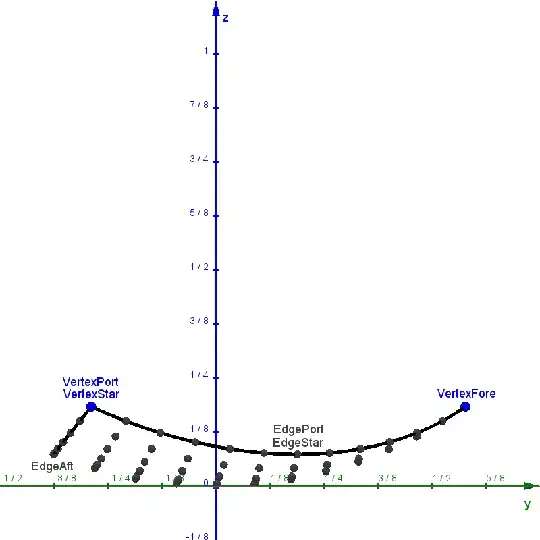
We can find the angle $β$ made by the aft-third points along $cThird$ and then rotate one of them around the center $2 (n − 1)$ times by an angle of $\frac{β}{2 n}$, generating equally-spaced points along the part of the circle that crosses the spherical patch. Taking rotations of those points about the $z$-axis and combining them with equally-spaced points along the boundary arcs, we can draw more circular arcs along the surface of the patch, each passing through two of the boundary points and one of the interior points. Intersections of these arcs give the remaining points of the triangulation:
This arrangement of points is more even than the first, with the longest edge between points only being about 1.4 times the length of the shortest, and it is still symmetrical. However, I have been unable to figure out how to go from this mostly-geometric construction to the required set of three parametric equations, even when going back to the "persevere despite/ignoring the mess" steps and slogging through the irreducible messes.