3

I always always been interested in learning about how to make my own Probability Distribution Function.

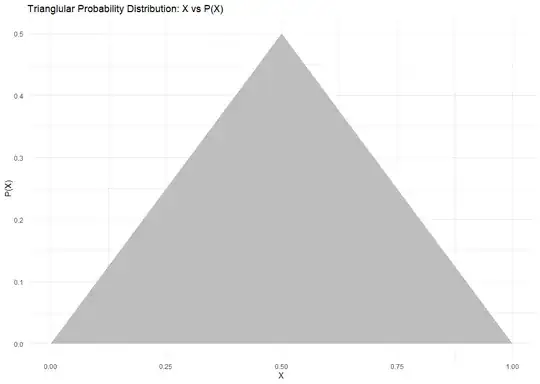
For example, suppose I want to make a Probability Distribution Function that looks like a triangle and has a peak at 0.5. This would look something like this:

library(ggplot2)

df <- data.frame(x = c(0, 0.5, 1, 0), y = c(0, 0.5, 0, 0))


ggplot(df, aes(x, y)) +
  geom_polygon(fill = "grey") +
  xlab("X") +
  ylab("P(X)") +
  ggtitle("Trianglular Probability Distribution: X vs P(X)") +
  theme_minimal()

enter image description here

I also know how to define this mathematically as a piece-wise function:

$$P(x) = \begin{cases} x & \text{if } 0 \leq x \leq 0.5, \\ -x + 1 & \text{if } 0.5 < x \leq 1. \end{cases}$$

However, there are some evident problems with this:

  • There is no way of guaranteeing that this function integrates to 1
  • This is a piecewise function and I do not think that a Probability Distributions can be defined in terms of piecewise functions

My Question: Is it possibly to take the work I have done and somehow modify it such that it becomes a valid probability distribution and integrates to 1?

Thanks!

Related Question:

stats_noob
  • 4,107
  • 1
    Your code and plot (slope $\pm 1$) don't match your formula (slope $\pm 2$). – aschepler Nov 14 '23 at 01:30
  • @ aschepler: thank you for pointing this out - I will revise this right now – stats_noob Nov 14 '23 at 01:31
  • You measure the grey area in your graph above (using classical geometry in this case, or an integral for more complicated distributions) and get $A = \frac 12 bh = \frac 14.$ Now you have some choices, make the peak higher, or the base wider, or some combination of both. – user317176 Nov 14 '23 at 01:32
  • 1
    There is no problem having a piecewise density. You do the integration and then rescale, so your $2x$ on $[0,\frac12]$ and $2(1-x)$ on $(\frac12,1]$ integrates to $\int_0^{1/2}2x,dx+ \int_{1/2}^1 2(1-x),dx=\frac14+\frac14=\frac12$ so you have to double everything to reach an integral of $1$, giving a density for your triangular distribution of $4x$ on $[0,\frac12]$ and $4(1-x)$ on $(\frac12,1]$ and $0$ elsewhere. – Henry Nov 14 '23 at 01:38
  • In fact triangular distributions are well-known. The sum of two i.i.d. uniform continuous random variables has a triangular distribution. – David K Nov 14 '23 at 01:40
  • @ Henry: thank you so much for your reply! I did not know this about piecewise functions – stats_noob Nov 14 '23 at 04:24
  • here is a related question I asked: https://math.stackexchange.com/questions/4804927/calculating-the-probabilities-of-a-100-sided-weighted-dice – stats_noob Nov 14 '23 at 22:57

1 Answers1

2

You can integrate the function over its domain.

In your case, since the function is piece -wise, it will be integrated piece wise.

Your function can be integrated using geometry (area under the curve). Using the standard formula for area of a triangle, it is $$\frac{1}{2}hb=\frac{1}{2}\times\frac{1}{2}\times1=\frac{1}{4}$$

Since you would like to make the area 1, you multiply the function by 4(reciprocal of 1/4).

In general, this is called the process of normalizing the function.

Note: I have used your graph, and not your piece wise function to answer. The two do not match. For example, 2x at 0.5 is 1, but the graph shows 0.5

Starlight
  • 2,684
  • Indeed, normalizing a thing generally means scaling it to unit magnitude. In the case of a vector v, we normalize it by dividing it by its norm $||{\bf v}||$. Not to be confused with the term normal; two vectors are normal to one another if their inner product is zero. – Paul Tanenbaum Nov 14 '23 at 01:35
  • @Starlight: Thank you so much for your answer! I have update the equation and graph - is this better? – stats_noob Nov 14 '23 at 05:18
  • Will this still result in a valid probability distribution function? – stats_noob Nov 14 '23 at 05:19
  • Once you normalize, yes, it results in a probability distribution. Normalization is a common process. For example, refer https://en.wikipedia.org/wiki/Normalizing_constant – Starlight Nov 14 '23 at 05:20
  • @Starlight: thank you so much for your reply! I want to make this triangle as a probability distribution function .... but the corresponding function is a piecewise a function. I have never seen a probability distribution that is written as a piecewise function. Is this possible? – stats_noob Nov 14 '23 at 22:01
  • here is a related question I asked: https://math.stackexchange.com/questions/4804927/calculating-the-probabilities-of-a-100-sided-weighted-dice – stats_noob Nov 14 '23 at 22:57