This partial answer relies on calculus. There are probably simpler solutions using more elementary methods. Slight adjustments need to be made to align with the pyramid you're actually using, but hopefully this serves as a decent starting point.
Let $S$ be the part of the sphere of radius $r$ bounded by the planes $z=k|x|$ and $z=k|y|$. By symmetry, the area of the spherical face is $4$ times the area of the part $S$ bounded by the planes $y=-x$ and $y=x$. The figure shows the phantom solid whose spherical face is $S$, and the quarter of it contained by $y=\pm x$ to either "side" and the plane $z=ky$ below. (Figure rendered with $r=k=2$; imagine the jagged edges are actually smooth)
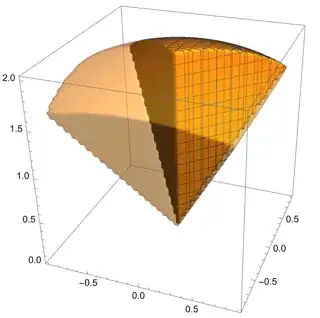
The factor $k$ indicates the ratio of the pyramid's height to half its base length. Parameterize $S$ in spherical coordinates by
$$\vec s(u,v) = r\cos(u)\sin(v)\,\vec\imath+r\sin(u)\sin(v)\,\vec\jmath+r\cos(v)\,\vec k$$
where $u\in\left[\frac\pi4,\frac{3\pi}4\right]$ and $v\in\left[0,f(u)\right]$. The upper bound on $v$ is obtained by finding the intersection of $x^2+y^2+z^2=r^2$ and $z=ky$ :
$$\begin{align*}
x^2 + \left(\frac zk\right)^2 + z^2 &= r^2 \\
r^2 \cos^2(u) \sin^2(v) + r^2 \left(1+\frac1{k^2}\right) \cos^2(v) &= r^2 \\
\sin^2(v) &= \frac1{k^2\sin^2(u)+1} \\[1ex]
\implies f(u) &= \arcsin\left(\frac1{\sqrt{k^2\sin^2(u)+1}}\right)
\end{align*}$$
Take the normal vector to $\vec s$ to be
$$\vec n = \frac{\partial \vec s}{\partial v} \times \frac{\partial \vec s}{\partial u} = r^2\cos(u)\sin^2(v)\,\vec\imath + r^2\sin(u)\sin^2(v)\,\vec\jmath + r^2\cos(v)\sin(v)\,\vec k$$
Then the surface element is
$$dA = \|\vec n\| \, du \, dv = r^2 \sin(v) \, du \, dv$$
and so the area of $S$ is given by the surface integral,
$$\begin{align*}
\iint_S dA &= 4r^2 \int_{\frac\pi4}^{\frac{3\pi}4} \int_0^{\operatorname{arccsc}\left(\sqrt{k^2\sin^2(u)+1}\right)} \sin(v) \, dv \, du \\
&= 8r^2 \int_{\frac\pi4}^{\frac\pi2} \int_0^{\operatorname{arccsc}\left(\sqrt{k^2\sin^2(u)+1}\right)} \sin(v) \, dv \, du
\end{align*}$$
(again, by symmetry). Adjust $k$ and the intercepts of the bounding planes as needed. Your pyramid does not have its vertex at the origin, rather on another sphere with radius slightly smaller than $r$.
