0

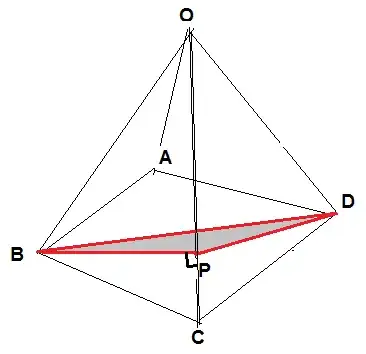
Let OABCD be a pyramid with square base ABCD such that the angle between lateral edge OA and OB,the angle between lateral edge OB and OC,the angle between lateral edge OC and OD,the angle between lateral edge OD and OA is $\frac{\pi}{4}$.Then what is the angle between the planes OAB and OBC,what is the angle between the planes OAB and ABC,and what is the volume of the pyramid.

EDIT 1:The sides OA=OB=OC=OD=1 unit

I dont have working knowledge of pyramids.Can someone please guide me how can i find the angle between lateral faces and angle between a lateral face and the base if the angle between the lateral edges is given.

Narasimham
  • 42,260
diya
  • 3,829

2 Answers2

1

The angle between two planes $\alpha$ and $\beta$, having a line of intersection $r$, is defined as the angle formed by two lines $a\subset \alpha$ and $b\subset\beta$, both perpendicular to $r$ at the same point $M$.

In your case, to find the angle between $OAB$ and $OBC$ you can for instance draw the altitudes $AM$ and $CM$ of those two faces: then the angle is $\angle AMC$. To compute it you can find the lengths of $AM$, $CM$ and $AC$ (by some standard trigonometry) and then use the cosine law to get the angle.

The angle between $OAB$ and $ABCD$ is even easier: if $OK$ is another altitude of face $OAB$, then the angle is just $\angle OKH$, where $H$ is the center of square base.

Intelligenti pauca
  • 55,765
  • In the book it is given,if $\theta$ is the angle between OA,OB,OC,OD taken in pair and if $\phi$ is the angle between $OAB$ and $OBC$,then $\sin^2\theta.\cos\phi=(1-\cos\theta)^2$.I did not understand how this relation was derived.@Aretino – diya Sep 29 '15 at 03:44
  • You can derive it by the method I outlined in my answer: I could go into further details but it's far better if you work a little on that. Ask if anything is not clear enough. – Intelligenti pauca Sep 29 '15 at 11:05
  • Using trigonometry in triangles OAB and OBC,i found AM and CM are $\sin\theta$ but i could not find $AC$ so that i could use cosine law in triangle AMC(M is meeting point as suggested in your post)@Aretino. – diya Sep 29 '15 at 11:30
  • 1
    Side $AB$ is $2\sin(\theta/2)$, so that $AC=\sqrt2 AB=2\sqrt2\sin(\theta/2)$. To recover the result given by your textbook you must use in the end the bisection formula $\sin^2(\theta/2)=(1-\cos\theta)/2$. – Intelligenti pauca Sep 29 '15 at 13:19
  • 1
    @Diya In isosceles triangle OCD, the angles are $ \pi/4, 3 \pi/8, 3 \pi/8 $ and normal PD is $ \cos \pi/8$. Is this much clear? – Narasimham Sep 29 '15 at 13:30
  • @Narasimham,yes i got it. – diya Sep 29 '15 at 13:31
  • @Narasimham,sir normal PD is coming$\sin \pi/4$.Isn't it? – diya Sep 29 '15 at 13:34
  • No, PD is $ \cos \pi/8 !! $ – Narasimham Sep 29 '15 at 13:40
  • When we consider triangle AMC,AM is $\sin\theta$,CM is $\sin\theta$,AC is 2$\sqrt2 \sin(\theta/2)$.Applying cosine law,\cos\phi=\frac{\sin^2\theta+\sin^2\theta-8\sin^2(\theta/2)}{2\sin^2\theta}=-\tan^2(\theta/2),but book says $\cos\phi=\tan^2(\theta/2)$,but i think we are nowhere wrong.@Aretino, – diya Sep 29 '15 at 13:41
  • Except the sign ! . It should be $ cos \phi =- tan^{2} \theta/2$ – Narasimham Sep 29 '15 at 13:58
  • Check: for $\theta=\pi/2$ you have $\phi=\pi$, so that $\cos\phi=-1$. So the formula in your book has the wrong sign. – Intelligenti pauca Sep 29 '15 at 14:56
1

Consider each face. Draw a diagram. Angles are $ \pi/4,3 \pi/8,3 \pi/8$ at top of pyramid and base respectively.

Draw a perpendicular onto a slant height side from any base corner (A,B,C or D) to a point labelled P. Its length is $ \cos \pi/8$. There are two such sides either side of dihedral indicated in a coarse sketch.

EDIT1:

The base of pyramid is taken as a unit square for convenience.

DihedralonPyramid

Base diameter is $ \sqrt 2$. Three sides are known, it is SSA case to solve for dihedral.

Use the Cosine Rule, simplify, getting angle

$$ \cos \gamma = -\tan^{2}\frac{\pi}{8}, \; \gamma \approx 99.8793^0 $$

Can you find pyramid height H ? Volume = H/3.

Narasimham
  • 42,260