Perspective view of longitudinal great circles - ellipses inside a circle

Question

I'd like to visualize the longitudes on a sphere from close-up, with correct perspective. It seems this is the "Blue Marble" problem i.e. to show how earth looks from a realistic distance (say 0.5 to 4 earth radii), and not from infinity with visible poles.

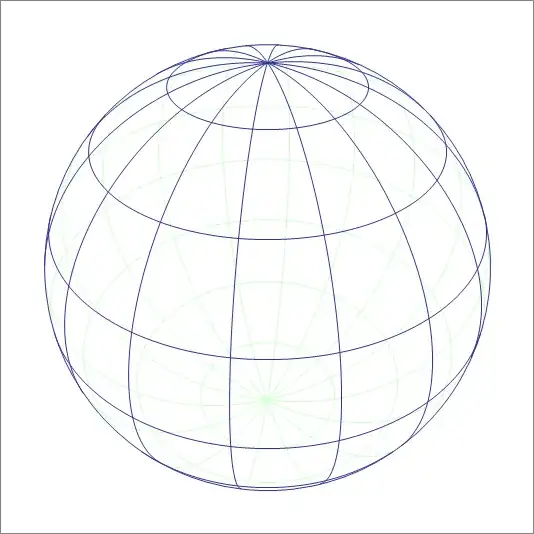
These are 6 ellipses fitted into the visible horizon. Note that the poles have both sunken below the horizon; the upper pole is marked by a small circle.

It is not easy to fit the ellipses into the circle by hand, because the center is shifted to the right, and both height and width have to be adapted.

I do have 5 points to nail it down: both poles, the chosen intersection with the x-axis, and the two tangent points with the circle. With only the y component of the center known (=0), I would start with this equation:

$$\frac{(x - x_o)^2}{a^2} + \frac{y^2}{b^2}=1$$

with the three unknowns $x_0, a$ and $b$.

The poles give two points on the ellipse.

Now I would add a chosen third point on the x-axis, for purple about (0.7, 0).

This leaves me with a bundle of ellipses: some wider than tall running to the left; some very high poking through the horizon, some too short to touch the circle from the inside.

I gather - and faintly recall from school - that I can find a single solution with a discriminant of zero.

So can anybody tell me how to proceed from here? Can it be done with (simple, maybe messy) algebra, or is there a shortcut? Do I have to find that 4th and symmetric 5th point first and then determine the ellipse?

Thank you

---

Added after comment:

Yes the uniform change in angle is important; now at least I can determine where I want the meridians (x-axis crossing would be a bit more practical), while by hand I had to leave them more or less where they fit.

My goal is to put the 0-degree and 41E-degree fulldisc satellite images side by side and stretch them so I can merge them with a straight 20.5 meridian. This works quite well, but only after I changed/softened the stretching point from 1-x (the circle) to 1-sqrt(x) by trial and error.

My graphic is meant as a test grid. I did not find anything similar on the internet. This is the usual perspective:

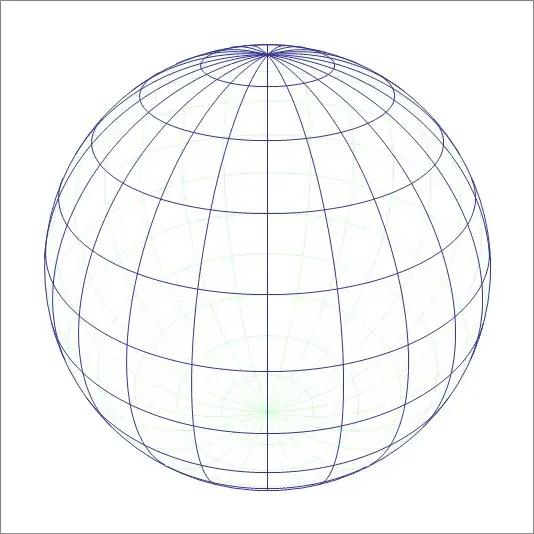
This is not central:

A "globe beach ball" from walmart comes - also literally speaking - closest:

And this is my result for now on youtube. The projection itself is not fantastic, but at least the seam in the middle is gone. There is also a "Mollweide" projection by NOAA where they combined East and West coast satellites.

But a correctly drawn complete grid would look nice on its own: shows the "fatness" of a sphere. That would be distance to determine the (un)visible poles, and degrees to choose the ellipse? I think that really is what I want!

Answer 1

Here's one way to do it. Assume the blue silhouette $c$ is the unit circle $x^2+y^2-1=0$, and that the poles are at $(0,\pm a)$. We wish to find the ellipse $e$ passing through the poles and tangent to the circle at the points that are the intersection of the circle with the line $x=b$, i.e. the points on the circle with $x$-coordinate $b$.

In general,when conics $c$ and $e$ touch (are mutually tangent) at two points $P,Q$ they are said to be in double contact. If $\ell=0$ is the equation of the line $PQ$, a conic in double contact with $c$ at the points $c\cap \ell$ is given by the equation $c+s\ell^2=0$ for some $s$. So in our case we need to solve for such a conic passing through the poles.

Here $\ell=0$ is the line $x-b=0$, so we are solving for $s$ such that $c+s\ell^2=x^2+y^2-1+s(x-b)^2=0$ passes through $(0,a)$. This gives us $s=\dfrac{1-a^2}{b^2}$.

So the family of ellipses corresponding to the perspective projections of circles of longitude is

$$ x^2+y^2-1+\dfrac{1-a^2}{b^2}(x-b)^2=0 $$

Note that values of $b$ in the interval $(-1,1)$ correspond to lines of longitude that are partially visible in this perspective. Values of $b$ outside of this interval will correspond to lines that are entirely occluded (i.e. on the far side of the silhouette).

Update (Feb 2024): A related question came up on $\mathbb X$ (formerly Twitter) recently - how to draw a perspective view of a planar slice of a quadric. The question and answer are in this $\mathbb X$ thread.

Answer 2

Not an answer, but to show what I got as the perspective projection of the longitudes. Some pointers on how I got this image are found in my comments above. The dark blue colored segments are the visible part of the projected longitudes while the gray segments are the invisible part. I've also added the globe latitudes in the following image where the gray color for the invisible segments has been replaced with light green. The third image has the meridians (the longitudes) symmetrical. The fourth image depicts the view observed $4$ times the radius of the sphere away from the center of the sphere, and lying on the equatorial plane.