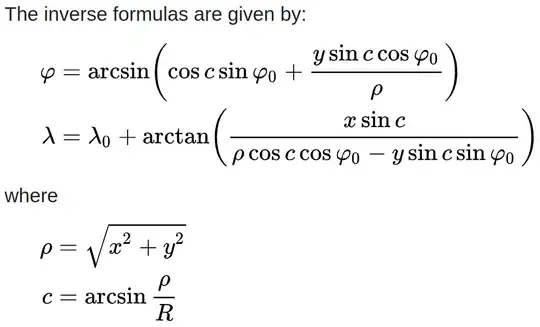How to get the exact cutoff angle for a given latitude in a spherical orthographic projection?

Question

I'm trying to compute a grid that's orthographically projected onto a sphere for the purposes of overlaying onto images of Sol (which is so far away that this is a good approximation), so that one can quickly see roughly the angular distance between certain points.

At first I wrote a simple program using basic knowledge of sines and cosines, and got a useful grid; however, the only reason this worked is because I did a projection centered on (0, 0), so I didn't have to account for tilt at all, and in that case all latitudes will simply have half of their longitudes visible.

This works perfectly fine for what I was trying to do, because the angular distances will still all be the same. That being said, now I've been trying to use the actual formulae for an orthographic projection so that I can incorporate tilt, since Sol's axis is tilted ~7.25 degrees with respect to the ecliptic. There's no need to adjust for longitudinal variation, because the images of Sol are all already rotated to account for this.

So, on this Wikipedia page I found the following:

I wrote up a program to project that, and this worked fine. I was still using a λ_0 and φ_0 of 0, so even without cutting off any points that are hidden behind the sphere it looked like the points were in the right places (since those behind simply overlapped with those in front). Then I adjusted λ_0 a little bit (again, φ_0 will remain 0 throughout all of this anyway), and could see how the points behind the sphere were visible. Thus I proceeded to the next part:

I implemented that too, and it worked perfectly, just as expected. All good so far, no problems at all. However, then I realized that what I wanted was a grid, not all these separate points. I tried for a bit to simply use a large number of points and draw lines between them, but this turned out to be a highly complicated endeavor due to the order the points get arranged in when projecting the original latitudes and longitudes in order, with a lot of lines cropping up that were not supposed to be there. In addition I thought this was a rather ugly solution anyway, even if I could work out the kinks, because my original grid had simply used curved lines (drawn as part of ellipses) and only needed a few different points defined for each line of latitude and longitude.

So then I read further down to this:

At first I thought that this was of no use to me, since this was (as far as I could tell) just a way of recovering the original grid of latitudes and longitudes from points that had already been projected. However, underneath I read this:

Now this seems to address the problem I'm encountering, but I couldn't, and still can't, understand exactly how. Essentially what I'm trying to do is, for any given latitude, I want to know what the cutoff angle is for a given latitude (λ), assuming a φ_0 of 0 and a given λ_0. That way I can simply draw partial ellipses based on this. However, now that I've though more about it, even this is further complicated by how the actual width of the whole ellipse I'm drawing parts of would also be significantly changed; if e.g. λ_0 is slightly positive, so the sphere is tilted upward, i.e. so you can see the south pole but not the north pole, then due to more longitudes being visible at lower latitudes, the ellipse widths there are smaller. Here's an image of what I mean, which I've generated using points:

In any case, I hope this is sufficient material to explain what I'm trying to achieve, i.e. to draw a grid with as few defined points as possible for each latitude and longitude given a certain tilt of central latitude (λ_0). To draw the original grid all I needed for each line was a partial ellipse defined by its center, width, height, and where to start and stop drawing along it, so something similar would be ideal, unless someone has better suggestions.

Edit:

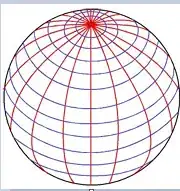
To clarify due to what's being asked in some comments, this is the type of grid I made intuitively using some simple sines and cosines at first, since the special case of being centered on (0, 0) simplifies a lot of things (and this works well for that original purpose):

https://i.postimg.cc/1sxvmRDz/solgrid.png

The problems arise when trying to incorporate the tilt, and to then still find simple parameters for drawing the partial ellipses that make up the "lines" (on the projection I guess they are better described as "curves" to be strict), rather than calculate a huge amount of points to try and draw straight lines between them in order to approximate both the edge and the curves.

Final edit:

The solution to this problem has been found, but I'm still trying to find the parameters for the resulting partial ellipses, so I've asked a new question for it here.

Answer 1

I will work this problem from a pure mathematical perspective for the most part (using an abstract sphere rather than the Sun and radians rather than degrees), but at the end we can relate it to your specific problem.

A key fact in this answer is that the points on a sphere that project onto the circumference of the sphere's image in an orthogonal projection are a great circle on the sphere, specifically, the great circle you get when you slice the sphere with a plane that passes through the sphere's center and is parallel to the projection plane. So your question comes down to, if we know the latitude of a point on that great circle, what is the longitude of that point?

Let's start by defining coordinates $\theta$ and $\lambda$ on the surface of the sphere. For consistency with mathematical formulas derived elsewhere, we will define $\theta$ as the colatitude (the angle measured along the surface from the "north pole" of the sphere) and $\lambda$ as the longitude (the angle that the point's line of longitude makes from the line of zero longitude). Working with colatitude rather than latitude may seem a little unusual, but that's the way many spherical geometry formulas are written, and it's easy to convert between colatitude and latitude when we need to.

In these coordinates, one equation describing a great circle (adapted from a post on MathOverflow) is

$$ \cot\theta = -\tan\theta_0 \cos(\lambda - \lambda_0) $$

where $\theta_0$ and $\lambda_0$ are the colatitude and longitude of a pole of the great circle. (A pole of a great circle is a point that has the same relation to the great circle as the north and south poles have to the equator. The right-hand side of the equation changes sign from the MathOverflow example because in this question we are "tilting" the axes in the opposite direction.)

Now, since we actually want to work with latitude rather than colatitude, we define the latitude $\phi$ as the angular distance on the sphere from the equator, so $\phi = \frac\pi2 - \theta$ and $\phi_0 = \frac\pi2 - \theta_0.$ With these substitutions, the equation of the great circle is

$$ \tan\phi = -\cot\phi_0 \cos(\lambda - \lambda_0). \tag1$$

So, given the latitude $\phi$ of a line of latitude on the sphere, we can solve Equation $(1)$ for $\lambda$:

\begin{align} \cos(\lambda - \lambda_0) &= -\tan\phi_0 \tan\phi, \\ \lambda - \lambda_0 &= 2\pi n \pm \arccos(-\tan\phi_0 \tan\phi) && \text{where $n$ is an integer}, \\ \lambda &= 2\pi n + \lambda_0 \pm \arccos(-\tan\phi_0 \tan\phi) && \text{where $n$ is an integer}. \\ \end{align}

The reason for the multiple solutions is that there are two longitudes where the line of latitude intersects the great circle, and the longitude can be measured in various ways. You might like to choose $n$ in such a way that $-\pi \leq \lambda \leq \pi,$ as we usually measure longitudes from $180$ degrees west to $180$ degrees east.

You actually have two choices for how to measure $\phi_0$ and $\lambda_0,$ because every great circle has two poles; but let's use the pole that we want to make visible in the projection. That is, $\phi_0$ and $\lambda_0$ are the latitude and longitude of the point that is projected into the exact center of the circle onto which the sphere is projected. Note that for a sphere with no axial tilt relative to the projection plane (so the equator projects to a straight line), $\phi_0 = 0$; if you tilt the axis so that the north pole is visible in the projection, then $\phi_0 > 0$; and if you tilt the axis so that the south pole is visible in the projection, then $\phi_0 < 0.$ In the image in the question, for example, $\phi_0 < 0.$

You might also want to take into account the fact that when the axis of the sphere is not parallel to the plane of projection, the projections of the poles will be inside the circle onto which the sphere is projected, and you will want to plot one of those poles (whichever one is "visible" to the observer) at the correct projected point.

At the point where that pole is projected, the projected images of $360$ degrees' worth of lines of longitude should all meet. That is, you want it to look something like this image from stackoverflow:

In order to avoid projecting parts of lines of latitude from the "non-visible" side of the sphere onto the projected image, you will want to cut off the image of every line of longitude at the same great circle where the lines of latitude are cut off.

That is, given the longitude $\lambda$ of a particular line of longitude, you want to solve for $\phi$ in Equation $(1)$ in order to find the latitude where the line of longitude has to be cut off:

$$ \phi = -\arctan(\cot\phi_0 \cos(\lambda - \lambda_0)). $$