As a bunch of answers on this site have pointed out: Can sum of two random variables be uniformly distributed, https://mathoverflow.net/q/228014/5429, the Uniform distribution is not divisible. That is, there is no distribution $D$, such that for iid. $X,Y\sim D$ the sum $X+Y$ is uniformly distributed.
This of course doesn't preclude that there is an "approximatively uniform" distribution, in some sense, that is divisible. An example might be the Generalized Normal Distribution, with pdf $\sim e^{-x^b}$ for some large even $b$. For $b\to\infty$ the distributino converges to the uniform distribution. Unfortunately the generalized normal distribution is only divisible for $b\in[0,1]\cup\{2\}$, so it is not of much help.
I'm wondering if there might be another family of distributions $D_{n\in\mathbb N}$ such that as $n\to\infty$ the pdf of $D_n$ converges point-wise to the indicator function $[-1 < x < 1]/2$, and where each $D_n$ is divisible?
If this is impossible, I'd also be interested in other measures of convergence, such as if the KL-Divergence between $D_n$ and $U$ goes to zero, $\mathrm{D}_\mathrm{KL}(D_n, U) \to 0$.
Update: I did some numerical optimization (with Total Variation loss) and got this funny looking approximation to the uniform distribution:
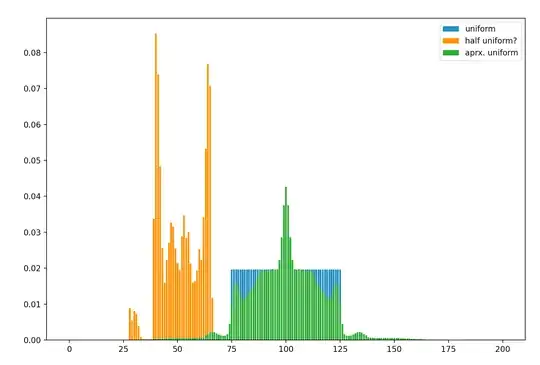With l2-loss, the optimal $D$ seems to be the normal distribution. I also tried JSD and the best distribution was approximately triangular.
With this is mind, I guess the right question is to ask: Which divisible distribution (in two iid. parts) has the smallest total variation distance to the uniform distribution?
