For questions about pointwise convergence, a common mode of convergence in which a sequence of functions converges to a particular function. This tag should be used with the tag [convergence].
A sequence of functions $f_n : X \to \Bbb{R}$ is said to converge pointwise to a function $f : X \to \Bbb{R}$ if $$ \lim_{n\to \infty}f_n(x) = f(x)$$ for all $x \in X$.
That is: $$\forall x \in X \forall \epsilon > 0 \exists N \in \Bbb{N}: \forall n \ge N, |f_n(x)-f(x)| < \epsilon.$$
In general, the pointwise limit is not a well-behaved operation. For example, the pointwise limit does not necessarily preserve the continuity of a function. Furthermore, the interchange of limit and integral signs does not hold in general: there exists functions $(f_n)$ with pointwise limit $f$ so that $\int_X f \ne \lim\limits_{n\to\infty} \int_X f_n$.
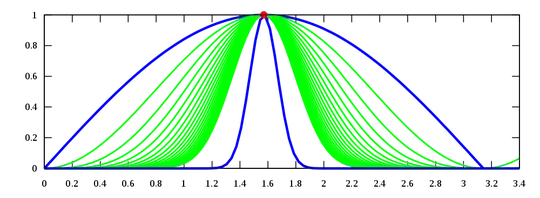The continuous functions $\sin^{n}(x)$ (in green) converge to a discontinuous function (in red).
Pointwise convergence is often compared with uniform-convergence. The later is stronger than the former, in the sense that uniform convergence implies pointwise convergence, while the reverse does not hold.
However, thanks to Egorov's Theorem in measure theory, pointwise convergence is almost uniform on sets of finite measure. That is, if $(f_n)$ are measurable functions defined on a measurable space, then pointwise convergence almost everywhere on a set $A$ of finite measure implies the apparently much stronger uniform convergence on $A \setminus B$, where $B$ is a set of arbitrarily small measure.
