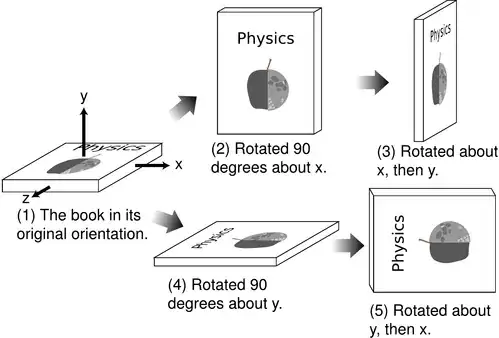
I'm trying to understand why the 3D rotation matrices are non commutative. I've searched for similar questions such as this one here
Why are rotational matrices not commutative?
Which explains very intuitively, that if you rotate around the X axis by 90 degrees, then around the Y axis by 90 degrees you end up in a different orientation than if you were to first rotate 90 degrees along Y then X.
This makes total sense, until I get to the Euler/Tait-Bryan Angles with "intrinsic" rotation.
If I rotate my pitch 90 degrees, then roll 90 degrees, I end up in the exact same orientation as if I were to roll 90 degrees then pitch 90 degrees.
What this tells me is that the order of rotations no longer matters, so the associated matrices should then be able to commute? I'm pretty sure this is incorrect, but I'm not sure I'm understanding why.