Tied chess matches and the monotonicity of $\sum_{k=0}^n \binom{2n}{k,k,2n-2k} (pq)^k (1-p-q)^{2n-2k}$

Question

In the upcoming World Chess Championship 14 games in the classical time format will be played compared to 12 in the previous matches. This change appears to have been made mainly to reduce the number of draws by allowing the players to take more risks, but it has also been stated that this decreases the chances of a tie in the overall series. Intuitively, this seems clear: the higher the total number of games, the less likely it is that both players win exactly the same number of games. A mathematical proof would be better, of course, and this is what I am after here.

I want to consider a simple model for the general case with $2n$ games, $n \in \mathbb{N}$. Let $p$ and $q$ be the probability for the first and second player to win any given game (independent of previous results, current form, etc.), respectively. Then $0 \leq p, q, p + q \leq 1$ holds and $1-p-q$ is the probability of a draw (we ignore the advantage for the player with the white pieces and interpret $p$ and $q$ as colour averages). Even though the series is not continued if one player takes an unassailable lead, we can pretend that all $2n$ games are played and compute the probability of $k$ wins for the first and $l$ wins for the second player from a trinomial distribution: \begin{equation} f(p,q,n;k,l) = \binom{2n}{k,l,2n-k-l} p^k q^l (1-p-q)^{2n-k-l} . \end{equation}

The probability of an overall tie is \begin{align} t(p,q,n) &= \sum \limits_{k=0}^n f(p,q,n;k,k) = \sum \limits_{k=0}^n \frac{(2n)!}{k!^2 (2n-2k)!} (pq)^k (1-p-q)^{2n-2k} \\ &= (1-p-q)^{2n} {}_2F_1 \left(\frac{1}{2}-n,-n;1;\frac{4 p q}{(1-p-q)^2}\right) . \end{align} Provided that this reasoning is correct, my question is:

How can we show that $t(p,q,n)$ is decreasing in $n$ for any given $p,q,p+q \in [0,1]$?

Some thoughts:

1. Numerically, this clearly appears to be true. This is the probability of a tie for $q=p$:
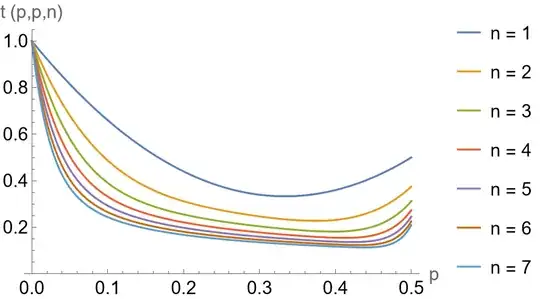
2. In the special case $p=q=\frac{1}{2}$ we have $$ t\left(\frac{1}{2},\frac{1}{2},n\right) = f\left(\frac{1}{2},\frac{1}{2},n;n,n\right) = \frac{1}{4^n} \binom{2n}{n} = \frac{2}{\pi} \int \limits_0^\infty \frac{\mathrm{d} x}{(1+x^2)^{n+1}} \, , $$ which is clearly decreasing in $n$.
3. Maybe an integral representation can also be helpful in the general case. I do not know a lot about hypergeometric functions though and cannot find a transformation which would allow us to use Euler's integral formula.

Answer 1

For convenience, define out-of-range multinomial coefficients as $0$. Let

\begin{gather*} r = 1 - p - q, \quad s = p + q, \\ a_k = 1 - \frac{1}{2k + 1} + \frac{1}{2n - 2k + 1}, \\ b_k = 1 + \frac{1}{2k + 1} - \frac{1}{2n - 2k + 1}, \\ c_k = r^2\frac{f(p, q, n; k, k)}{f(p, q, n + 1; k, k)} = \frac{(2n - 2k + 2)(2n - 2k + 1)}{(2n + 2)(2n + 1)}, \\ d_k = 4pq\frac{f(p, q, n; k - 1, k - 1)}{f(p, q, n + 1; k, k)} = \frac{4k^2}{(2n + 2)(2n + 1)}. \end{gather*}

Since $r^2 + a_krs + b_krs + s^2 = r^2 + 2rs + s^2 = 1$, we have

\begin{split} t(p, q, n) &= \sum_{k=0}^n f(p, q, n; k, k) \\ &= \sum_{k=0}^{n} (r^2 + a_krs) f(p, q, n; k, k) + \sum_{k=0}^{n} (b_krs + s^2) f(p, q, n; k, k) \\ &= \sum_{k=0}^{n + 1} ((r^2 + a_krs) f(p, q, n; k, k) + (b_{k-1}rs + s^2) f(p, q, n; k - 1, k - 1)) \\ &= \sum_{k=0}^{n + 1} \left((r^2 + a_krs)\frac{c_k}{r^2} + (b_{k-1}rs + s^2)\frac{d_k}{4pq}\right)f(p, q, n + 1; k, k) \\ &≥ \sum_{k=0}^{n + 1} \left((r^2 + a_krs)\frac{c_k}{r^2} + (b_{k-1}rs + s^2)\frac{d_k}{s^2}\right)f(p, q, n + 1; k, k) \\ &= \sum_{k=0}^{n + 1} \left(c_k + a_kc_k\frac sr + b_{k-1}d_k\frac rs + d_k\right)f(p, q, n + 1; k, k) \\ &≥ \sum_{k=0}^{n + 1} (c_k + 2\sqrt{a_kb_{k-1}c_kd_k} + d_k)f(p, q, n + 1; k, k) \\ \end{split}

We claim $c_k + 2\sqrt{a_kb_{k-1}c_kd_k} + d_k ≥ 1$; this is trivial if $k = 0$ ($c_k = 1, d_k = 0$) or $k = n + 1$ ($c_k = 0, d_k > 1$), and otherwise, it follows from

\begin{multline*} 4a_kb_{k-1}c_kd_k - (1 - c_k - d_k)^2 \\ = \frac{k^2(2n + 2(n - k) + 5)(4(2n + k + 1)(n - k) + 10n + 7)}{(2n + 1)^2(n + 1)^2(2(n - k) + 3)(2k + 1)(2k - 1)} ≥ 0, \end{multline*}

since every factor on the right is nonnegative. Therefore,

\begin{split} t(p, q, n) &≥ \sum_{k=0}^{n + 1} f(p, q, n + 1; k, k) = t(p, q, n + 1). \end{split}

Answer 2

Not an answer but a reformulation.

The problem can be stated as a random walk $X_n$ , starting at $X_0=0$ and with $X_n = X_{n-1} + Z_n$ where $Z_n$ is iid taking values over $\{-1,0,1\}$ with given probabilities $p_{-1}=q>0$, $p_{0}=1-(p+q)$, $p_1 = p>0$.

We want to prove the conjecture $P(X_{2(n+1)} = 0) < P(X_{2n} = 0)$

This seems particularly non-obvious for small $n$. For large $n$, one expects (by the CLT) that

$$P(X_{2n}=0) \approx \frac{1}{\sqrt{4\pi n\sigma^2}} \exp \left( - \frac{2n\mu^2}{\sigma^2}\right)$$

where $\mu = p-q$ and $\sigma^2=p+q-(p-q)^2$, provided that $p+q<1$. Elsewhere, for $p+q=1$ it should be multiplied by $2$.

Granted, this says little about the conjecture in itself.