What is wrong with my approach to solve 'The hurried duellers' problem?

Question

This is the problem statement :

Duels in the town of Discretion are rarely fatal. There, each contestant comes at a random moment between 5am and 6am on the appointed day, and leaves exactly 5 minutes later, honor served, unless his opponent arrives within the time interval and then they fight. What fraction of duels lead to violence?

This was my approach :

• Let's say A,B are the two duellers, then the probability of A arriving first would be the same as B arriving first, let's calculate the probability of duel happening if A arrives first.

• Since A arrives first if He arrives in 55-60 interval, there's definitely going to be a duel.

• If A arrives in 0-55 interval, the probability would be given by

$$\int_0^{55} \frac{5}{(60-x)} dx$$

Now let's call this above probability $p$, then the actual probability would be give by :

$$\frac{p}{2} + \frac{p}{2}$$

as half is probability of A arriving first and then same calculation with B arriving first.

But this approach doesn't give correct result.

I know this problem has been asked here : The Hurried Duelers brainteaser

And I also know another approach to solve the problem.

But i want to understand what I'm doing wrong in my calculation.

EDIT : The answer is supposed to be approximately ~23/144,

But I get much larger value.

Answer 1

Addendum-2 added to demonstrate the pure Calculus approach that more closely aligns with the original poster's (i.e. the OP's) approach.

---

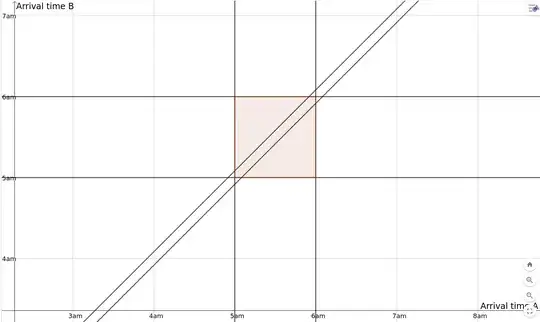
Your approach assumes that under the assumption that A arrives first, each 5 minute interval of time where A arrives is equally likely. This is false.

For example, while the normal probability of A arriving in the 55-60 interval is $(1/12)$, the probability of A arriving in the 55-60 interval is not $(1/12)$ under the assumption that A arrives before B.

---

Therefore, the problem is best attacked without making an assumption of who arrives first, as follows:

$\underline{\text{Case 1: A arrives in the interval of} ~~5 - 55}$
The chance of this occurring is $(50/60) = (5/6)$.
When it does occur, the chance of a meeting is $(10/60) = (1/6).$
Therefore, the computation that covers Case 1 is
$T_1 = (5/6) \times (1/6) = (5/36).$

$\underline{\text{Case 2: A does not arrive in the interval of} ~~5 - 55}$
As discussed in Case 1, the chance of Case 2 occurring is $(1/6)$.
When Case 2 occurs, you can assume, on average that A's arrival time is exactly 2.5 minutes from one of the boundaries.
That is, you can assume that A arrives either 2.5 minutes after the start of the hour, or 2.5 minutes before the end of the hour.
Under this assumption, B has an intersection interval of 7.5 minutes rather than 10 minutes.
Therefore, the computation that covers Case 2 is
$T_2 = (1/6) \times (7.5/60) = (1/6) \times (1/8) = (1/48).$

---

Final answer:

$$T_1 + T_2 = (5/36) + (1/48) = (23/144).$$

---

Addendum
Actually, in Case 2, I pulled an accurate but (arguably) invalid fast one.

That is, I assumed that Without Loss of Generality, in Case 2, A arrived exactly 2.5 minutes from one of the boundaries. I knew that this shortcut would result in the right answer, because I knew that the computation is linear. In fact, the rigorous approach for Case 2, would be to set up a Calculus problem. To me, in this instance, that is (arguably) overkill.

Consider the related problem:
What is the area under the curve $f(x)$ for the region $0 \leq x \leq 1$, where $f(x)$ equals $x$.

Technically, you are supposed to compute $\int_0^1 xdx.$

However, since the area function is linear to height, and since the average height of the function is $(1/2)$, I know from experience that the area of the region is $(1/2) \times (1-0).$

I took the same sort of (invalid) shortcut in Case 2.

---

Addendum-2
I was curious about the pure Calculus approach.
Never having formally studied probability, I had to guess about how to use a probability density function. My guesswork is below.

Without Loss of Generality, label the first person to arrive as $A$, and the 2nd person to arrive as $B$. This means that it is assumed that $A$ arrives on or before $B$. Then the probability of a duel will be expressed as

$$\frac{N\text{(umerator)}}{D\text{(enominator)}}$$

where $N$ will represent the integral, as $x$ goes from $0$ to $60$ of $p(x) \times f(x)$ and $D$ will represent the integral as $x$ goes from $0$ to $60$ of $p(x)$.

This means that $N$ will represent integrating, at each point $x$, the product of the relative chance of $A$ arriving at time $x$, times the chance of a duel, given that $A$ arrived at time $x$.

$D$ will represent the integral at each point $x$ of the relative chance of $A$ arriving at time $x$. Thus, $D$ will be used to normalize the relative probabilities.

Note further, that one of the two people had to be the first to arrive, and that this first arrival is arbitrarily given the label of $A$. This indicates that once the computations are completed, it is inappropriate to then multiply the computations by $(2)$, as the OP did.

For the first person to arrive at time $x$, this means that the 2nd person had to arrive at any time in the interval $(60 - x).$

Thus, it is reasonable to let the relative probability $~\displaystyle p(x) = \frac{60 - x}{60}$.
This implies that
$\displaystyle D = \int_0^{60} \frac{60 - x}{60} dx ~=~ \frac{60x - (x^2/2)}{60} ~{\Large{|_{0}^{60}}} = 30.$

Specifying the conditional probability of $f(x)$ is tricky, since it assumes that the 2nd person has arrived in the interval between $x$ and $60$. Therefore:

For $0 \leq x \leq 55, f(x) = \frac{5}{60 - x}.$
For $55 \leq x \leq 60, f(x) = 1.$

Therefore $N$ equals

$$\int_0^{55} p(x)f(x)dx + \int_{55}^{60} p(x)f(x)dx$$

$$= \int_0^{55} \frac{60 - x}{60} \times \frac{5}{60 - x} ~dx + \int_{55}^{60} \frac{60 - x}{60} ~dx$$

$$= \frac{x}{12} ~{\Large{|_{0}^{55}}} + \frac{60x - (x^2/2)}{60} ~{\Large{|_{55}^{60}}} $$

$$= \frac{55}{12} + \frac{3600 - 1800}{60} - \frac{3300 - 1512.5}{60}$$

$$= \frac{(55 \times 10) + (1800 \times 2) - (3575)}{2 \times 60} = \frac{575}{120}.$$

Therefore

$$\frac{N}{D} = \frac{575}{120 \times 30} = \frac{23}{144}.$$

Answer 2

Here is a diagram of the arrival times. The arrival times of A and B are on the $x$ and $y$ axes respectively. The square represents them both arriving between 5am and 6am. The space between the two diagonal lines (lying five minutes above and below the main diagonal, respectively) represents them arriving within 5 minutes of one another.

So what we actually want to know is, given that a point is chosen uniformly at random from the highlighted square, what is the probability that it lies between the two diagonal lines?

It's not a very difficult geometry problem. Your idea of looking at when A arrives first corresponds to restricting ourselves to the region above the main diagonal of the square. Which still, if done correctly, gives the correct probability, not half the probability.

Answer 3

You did not specify how you combine the probability for the $55$ to $60$ minute case with the probability for the $0$ to $55$ minute case, but based on your treatment of the $0$ to $55$ minute case I guess you assumed that when A arrives first, the $0$ to $55$ minute case happens $11$ out of $12$ times and the $55$ to $60$ minute case happens $1$ out of $12$ times.

Taking a loot at your calculation for the $0$ to $55$ minute case, it appears that you (correctly!) supposed that if A arrives at $x$ minutes past 5 am, there is a $5/(60 - x)$ probability of a duel. Given that conclusion, and assuming that A is equally likely to arrive within any $t$-second interval of the $55$-minute period, given that A arrived first, you would conclude that the probability of a duel in the case of A arriving first and arriving between 5 am and 5:55 am is

$$ \frac{1}{55} \int_0^{55} \frac{5}{60-x}\, \mathrm dx. $$

That's the correct probability under the "equally likely" assumption that I have shown with emphasis in the previous paragraph. Since it's the same as your formula (apart from the factor $1/55$) I guess that's how you obtained your formula, and the factor $1/55$ was in the part of the calculations you did not tell us about. (If you don't have that factor, you get a probability greater than $12$, clearly impossible.)

Where you go wrong is when you make that assumption, because A is not equally likely to arrive within any $t$-second interval given that A arrives first. The probability that A arrives between 5 and 5:05 am and arrives first is

$$ \frac{1}{12} \int_0^5 \frac{60-x}{60} \,\mathrm dx = \frac{115}{288} \approx 0.399, $$

whereas the probability that A arrives between 5:50 and 5:55 am and arrives first is

$$ \frac{1}{12} \int_0^5 \frac{60-x}{60} \,\mathrm dx = \frac{5}{96} \approx 0.052. $$

So in fact, given that A arrives first, the case in which A arrives between 5 and 5:05 am is much more likely than the case in which A arrives between 5:50 and 5:55 am. It is not correct to give equal weight to those two cases, but that's apparently what you did.

If you also treated the $55$ to $60$ minute case similarly, you acted as if it is much more likely for A to arrive in the last five minutes of the hour and still be the first to arrive than for A to arrive in the first five minutes and be first, whereas actually the second case is twice as likely to occur.

You can correct the error by weighting each probability for B to arrive in time for a duel by the probability density of A being the first to arrive, given that A arrives at $x$ minutes past the hour. But I think it's much easier not to consider the case where A arrives first separately from the case where B arrives first. instead, consider the case where A arrives in the first five minutes ($0 \leq x \leq 5,$ probability $(x + 5)/60$ of a duel), the case where A arrives in the last five minutes ($55 \leq x \leq 60,$ probability $(55 - x)/60$ of a duel), and the case where A arrives between 5:05 and 5:55 ($5 < x < 55,$ probability $10/60$ of a duel). Because we're not adding any other assumptions such as "A arrived first" in any of those cases, it's legitimate to suppose that A is equally likely to arrive in any $t$-second interval as any other $t$-second interval.

Easier still is Arthur's graphical approach (also hinted by Henry's answer to the linked question), which is equivalent but easier to compute.

Note that no matter when A arrives, there is only a $10$-minute period during which B could arrive and cause the duel to occur (up to five minutes before A and up to five minutes after A). Since B's arrival time is randomly (presumably uniformly) distributed between 5 am and 6 am, there is at most a $1/6$ probability for B to arrive within the necessary $10$-minute interval around A's time of arrival. (Less than $1/6$ if A arrived before 5:05 or after 5:55). Even if you did not have access to an answer key, you should still check any calculations against that upper bound.