9

In the equilateral triangle below, $CD, AD$, and $BD$ concur at point $D$. The measures of the angles ($a, b, c, d, e,$ and $f$) are also defined as given in the figure below. Conjecture: There aren't any $a, b, c, d, e,$ and $f$ such that all are different integers without using the combinations of the numbers: $6, 54, 42, 18, 48$, and $12$. (to clarify, all six of these numbers can not be used together, but they can be used together in groups) How can I prove this conjecture mathematically, and what is so special about these six numbers? enter image description here

My thoughts and work on the problem

I am intentionally omitting the degree signs for convenience.

Using, the Trigonometric Ceva's Theorem, I obtained the following expression:

$$\frac{\sin(a)}{\sin(b)}\cdot\frac{\sin(c)}{\sin(d)}\cdot\frac{\sin(e)}{\sin(f)}= 1$$

which is equivalent to: $$\begin{aligned} \sin(a) \sin(c) \sin(e) = \sin(b) \sin(d) \sin(f) \end{aligned} \label{a}\tag{1}$$

We also know that,

$$a+b=c+d=e+f=60$$

To convert the triple sine product to summations, I used the following "trick". Since, $$\sin(a+c+e)=\sin(b+d+f)$$

and also due to $Eq. (1)$, it is true that: $$\sin(-a+c+e)+\sin(a-c+e)+\sin(a+c-e)$$

$$=\sin(-b+d+f)+\sin(b-d+f)+\sin(b+d-f)$$

Let's substitute $b=60-a, d=60-c$, and $f=60-e$ and let $x=(c+e-a), y=(a+e-c),$ and $z=(a+c-e)$ to simplify things a bit:

$$\sin(x) +\sin(y) +\sin(z)=\sin(60-x)+\sin(60-y) +\sin(60-z)$$

I expanded the $(60-x)$'s using compound angle formulae:

$$\sqrt{3}/2 (\cos(x) + \cos(y) + \cos(z)) - 3/2 (\sin(x) + \sin(y) + \sin(z)) = 0$$

which simplifies to:

$$\sin(30-x) +\sin(30-y) +\sin(30-z)=0$$

but I feel lost in the algebra and don't know what to do next. I want to get to a point where I can easily plug numbers and show that no other numbers satisfy this equation, other than the combinations of the six numbers given at the beginning.

The trigonometric proof of one of the cases may aid to formulate a proof, so I decided to include it as well: For $a=6, b=54, c=42, d=18, e=48, f=12$, $Eq. (1)$ is satisfied, so let's prove it.

Proof. $$ \sin(12°) \sin(18°) \sin(54°)\stackrel{?}{=} \sin(6°)\sin(42°)\sin(48°)$$ Now we use the "trick": $$ \sin(60°)+ \sin(48°)- \sin(24°)\stackrel{?}{=} \sin(84°)+\sin(12°)+\sin(0°)$$ $$\sin(60°)=\frac{\sqrt{3}}{2} \stackrel{?}{=} \sin(12°)+ \sin(24°) - (\sin(48°) -\sin(84°))$$ $$ = 2 \sin(18°) \cos(6°) + 2 \cos(66°) \sin(18°)$$ $$ = 2 \sin(18°) (\cos(6°) + \cos(66°)$$ $$ = 2 \sin(18°) (2\cos(36°)\cos(30°) )$$ $$1 \stackrel{?}{=} 4 \sin(18°) \cos(36°)$$ $$\frac{1}{2} = \cos(36°) \cos(72°)$$ which is true as it is a well-known identity.

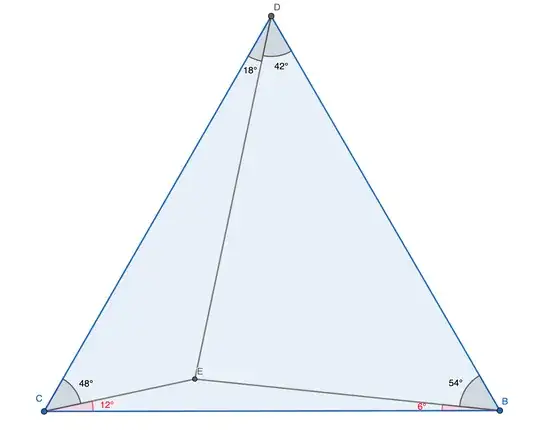
Here is the figure of this triangle (rotated): enter image description here

Given only 6 and 12 degrees (the red angles) the rest of the angles can be found. For the sake of brevity, I will omit the synthetic proofs. For the interested reader, see this link, as it also shows the beauty of synthetic solutions in these types of problems from the perspective of a geometrician. The combinations of $6, 54, 42, 18, 48$, and $12$ often come up in synthetic geometry problems: I even managed to find one in SE.

@KorayUlusan helped me develop a code to test the conjecture by brute force in Python. Turns out that the conjecture is correct, but I'm looking for a mathematical explanation. Here is the code:

import math

epsilon = 2.22044604925e-14  # for integer overflow


for a in range(60):
    b = 60 - a  # because a+b=60
    for c in range(60):
        d = 60 - c
        for e in range(60):
            f = 60 - e
            if a != b and b != c and c != d and d != e and e != f:

                try:
                    rightHandSide = (
                        math.sin(math.radians(a))
                        * math.sin(math.radians(c))
                        * math.sin(math.radians(e))
                    ) / (
                        math.sin(math.radians(b))
                        * math.sin(math.radians(d))
                        * math.sin(math.radians(f))
                    )


                if abs(1 - rightHandSide) < epsilon:
                    print(f"a is {a}, b is {b}, c is {c}, d is {d}, e is {e}, f is {f}")

            except ZeroDivisionError:
                pass

The Python output for the code (of course, most of these results are the same triangles, just rotated):

a is 6,  b is 54, c is 42, d is 18, e is 48, f is 12
a is 6,  b is 54, c is 48, d is 12, e is 42, f is 18
a is 12, b is 48, c is 18, d is 42, e is 54, f is 6 
a is 12, b is 48, c is 54, d is 6,  e is 18, f is 42
a is 18, b is 42, c is 12, d is 48, e is 54, f is 6 
a is 18, b is 42, c is 54, d is 6,  e is 12, f is 48
a is 42, b is 18, c is 6,  d is 54, e is 48, f is 12
a is 42, b is 18, c is 48, d is 12, e is 6,  f is 54
a is 48, b is 12, c is 6,  d is 54, e is 42, f is 18
a is 48, b is 12, c is 42, d is 18, e is 6,  f is 54
a is 54, b is 6,  c is 12, d is 48, e is 18, f is 42
a is 54, b is 6,  c is 18, d is 42, e is 12, f is 48

Thanks in advance for any sort of help or contribution.

krazy-8
  • 2,294
  • Degrees are not a natural measure for angles. – user Mar 16 '21 at 09:06
  • I find the statement of your conjecture baffling. Why is $a = 1^\circ$, $b = 59^\circ$, $c = 2^\circ$, $d = 58^\circ$, $e = 3^\circ$, $f = 57^\circ$ not a solution? These are all integers and are without any combinations of the numbers: $6$, $54$, $42$, $18$, $48$, and $12$ (by not including any of them). All your code does is force $a+b = c+d = e+f = 60^\circ$, then verify that you have an equilateral triangle, which is literally what you have enforced. There is no check for any of the numbers $6$, $54$, $42$, $18$, $48$, or $12$. – Eric Towers Mar 16 '21 at 09:07
  • @EricTowers But your solution doesn't satisfy the ceva's theorem ($Eq.(1)$), which means that it is not possible to construct an equilateral triangle with such angles. Being given angles $a$ and $c$ is enough to determine the other angles. – krazy-8 Mar 16 '21 at 09:13
  • First, the conjecture does not mentoin Ceva's theorem, so no solution is required to have any relationship with that theorem. Second, an equilateral triangle has three $60^\circ$ angles and my example, using your labelling in the first diagram, has three $60^\circ$ angles, giving an equilateral triangle. Your claim that it is not equilateral is unintelligible. – Eric Towers Mar 16 '21 at 09:17
  • @EricTowers With all respect, what I’m trying to say is that it is not possible to arbitrarily assign values to all angles. For example see this problem: https://math.stackexchange.com/questions/995421/finding-an-angle-between-side-and-a-segment-from-specified-point-inside-an-equil We can find the other angles different than 6 and 12 by geometry or trigonometry, so the triangle is already defined. Trigonometric Ceva holds in all triangles. In my problem, although the only condition is that the angles sum to 60 at vertices, you have to assign values such that the trigonometric ceva will hold. – krazy-8 Mar 16 '21 at 09:32
  • 1
    Please point out where "trigonometric Ceva's theorem" appears anywhere in your statement of your conjecture: "For the equilateral triangle below, there aren't any a,b,c,d,e, and f such that all are different integers without using the combinations of the numbers: 6,54,42,18,48, and 12. (to clarify, all six of these numbers can not be used together, but they can be used together in groups) How can I prove this conjecture mathematically, and what is so special about these six numbers?" If you don't state it as a condition, it is not a condition. – Eric Towers Mar 16 '21 at 09:40
  • You could also mention "concurrent Cevians" as a condition. But there is nothing in the statement of the conjecture that references any version of Ceva's theorem. – Eric Towers Mar 16 '21 at 09:44
  • @EricTowers I admit that I have not stated the conjecture properly in words, but I thought that it was obvious from my statement “for the given equilateral triangle below” and from my work on the problem. I have now edited, hopefully it is more clear now. – krazy-8 Mar 16 '21 at 10:31

1 Answers1

2

Not an answer but an extended comment.

First: you have already proved the conjecture. You may think that the exhaustive search is not a nice tool, but you checked all $59\times 59\times 59$ possibilities and proved that there are no other solutions.

Second: there is no mystics about the integer numbers. They appear to be integer because some ancient human being decided that it is nice to divide the circle in 360 parts which were named "degrees". The obtained solutions would remain integer if he/she decided to divide it instead in 60 parts but cancel to be integer if he/she would prefer 100 parts.

Third: the problem can be however formulated as a really challenging one.

The following formulation of the problem is due to @Blue

Namely: find all triples $\{p,q,r\}$ of non-zero rational multiples of $\pi$: $$-\frac\pi6 <p,q,r<\frac\pi6$$ such that $$ \sin\left(\frac{\pi}{6}+p\right) \sin\left(\frac{\pi}{6}+q\right) \sin\left(\frac{\pi}{6}+r\right) = \sin\left(\frac{\pi}{6}-p\right) \sin\left(\frac{\pi}{6}-q\right) \sin\left(\frac{\pi}{6}-r\right)\tag1 $$ which neatly reduces to: $$ \cot p\cot q+\cot q\cot r+\cot r\cot p=−3.\tag2 $$

I have checked all triplets with denominator up to $n=120$ and the result is: there are no others except for $$ \frac\pi{30}\{2,3,-4\}, $$ which you have found. Is the triplet the only one?

user
  • 27,958
  • 2
    For balance and simplicity, I would express the angles as $\frac\pi6\pm p$, $\frac\pi6\pm q$, $\frac\pi6\pm r$ for $p$, $q$, $r$ non-zero rational multiples of $\pi$ with distinct absolute values. Then the Ceva criterion $$\sin\left(\frac\pi6+p\right)\sin\left(\frac\pi6+q\right)\sin\left(\frac\pi6+r\right)=\sin\left(\frac\pi6-p\right)\sin\left(\frac\pi6-q\right)\sin\left(\frac\pi6-r\right)$$ reduces neatly to $$\cot p\cot q+\cot q\cot r+\cot r\cot p=-3$$ The question becomes: Are there solutions besides OP's ${p,q,r}=\pm\frac\pi{180}{12,18,-24}$? – Blue Mar 16 '21 at 13:25
  • This looks really nice! May I incorporate this in my answer? – user Mar 16 '21 at 13:38
  • Sure! :) ...... – Blue Mar 16 '21 at 13:39
  • I don't see a reason to restrict $p$, $q$, $r$ to $(-\pi/6,\pi/6)$. Ceva's theorem works for points of concurrency outside the triangle. I think we need ask that they none equals $0$ (trivial) or $\pm\pi/6$ (degenerate), but otherwise require only that they're acute in absolute value. ... Also, you left out the criterion of distinct absolute values (which corresponds to OP's requirement of six distinct individual angles); I haven't thought hard enough about the ramifications of that condition. (Certainly, $p=-q$ and symmetry force the trivial case $r=0$. Is $p=q$ (un)interesting?) – Blue Mar 16 '21 at 15:01
  • The question of OP certainly concerns only about an inner point of the triangle. But of course this restriction can be removed. What concerns the requirement of six distinct angles I am pretty sure it was aimed on removing the multiple solutions with the angle $\frac\pi6$. In your formulation it is replaced with the requirement of being non-zero. – user Mar 16 '21 at 15:19
  • "The non-zero requirement isn't equivalent to forbidding $\pi/6$ angles." Why? Setting $p=0$ is equivalent to drawing the angle bisector (i.e. the corresponding angle equal to $\frac\pi6$). Certainly in this case two other angles can take on any (opposite) values. – user Mar 16 '21 at 16:24
  • Whoops ... Got my thoughts mixed. What I meant to write was that the non-zero requirement isn't equivalent to the six-distinct-angles requirement, the latter of which may (or may not) ignore additional non-trivial solutions. ... The point that, along with focusing on integer-degree angles and interior concurrency points, OP may be artificially restricting the problem and inadvertently overlooking some interesting possibilities. – Blue Mar 16 '21 at 16:37
  • I can only repeat my previous statement that in my opinion OP has in mind only to avoid the trivial solution with $\pi/6$ angle. And since no other "rational" solutions to the equation (2) are so far found there is no reason to argue whether we should accept such a solution. :) In this sense it is preferable to keep the space for the new solutions as wide as possible. It seems that the requirement of being rational fraction of $\pi$ is extremely strong by itself. – user Mar 16 '21 at 16:46
  • @user Firstly, thank you for this extended discussion. I must say that my main interest is in geometry, and “given two non-adjacent angles find \alpha” types of questions come up again and again on various websites and on various books. I completely understand what you mean by degrees not being a natural measure for angles, but I was hoping there would be some analytical method (maybe a proof by cases), when I obtained the following equation: $\sin(\pi/6-x) +\sin(\pi/6-y) +\sin(\pi/6-z)=0$ – krazy-8 Mar 17 '21 at 04:02
  • I should probably add this also to the body, but to give some context, what I actually have in mind is the generalized problem: Suppose we were to only remove the restriction of being an equilateral triangle (which probably deserves to be a separate question). Using a computer to find all such solutions seems to be more complicated than the initial problem (with equilateral condition), but much easier than trying to find analytically (which I hope is possible). This time being given two non-adjacent angles is not enough to define the triangle from a geometric perspective. – krazy-8 Mar 17 '21 at 04:08
  • @Blue I come across your geometry solutions every once in a while and thank you for helping. This is the part where I’m mainly interested: I suspect synthetic geometric solutions can be provided for all of these integer angled (non-equilateral) triangles given two pairs of adjacent angles. My main motivation is to collect all of these triangles together and classify them into groups. I suspect it will possible to group them according to their synthetic solutions. – krazy-8 Mar 17 '21 at 04:12
  • 1
    @dodoturkoz If one insists that the triangle angles have to be "integer" in degrees it is not difficult to test all possible $59\times 59$ "general" triangles. – user Mar 17 '21 at 06:38
  • @dodoturkoz Addendum to my last comment. A test has shown that there are a lot of such "integer" cases. If one codes them by sextuplets of Ceva's angles $((a_1,b_1,c_1),(a_2,b_2,c_2))$ (which give upon permutation up to 6 different triangles) the triangle with the smallest possible angle has the solution $((1,30,87),(2,29,31))$. Can you start with the numbers? – user Mar 17 '21 at 11:33
  • @user Here is the triangle: https://i.sstatic.net/HGDoa.png My goal is to use the bottom four angles to obtain the 1 and 2 degrees via some miraculous synthetic geometry solution. The 30° angle increases my faith, but it still looks very difficult. I don’t know which of these sextuplets (as I assume there are more) are solvable via synthetic geometry and proving whether it is possible seems like an incredibly difficult task. I suspect the ones containing 30° or 60° or other “nice” angles may allow certain constructions, however the rest may just be “unsolvable”. Thank you so much. – krazy-8 Mar 17 '21 at 13:10
  • @dodoturkoz Actually one can construct 6 different triangles from this sextuplet. And there are hundreds of others (at least one sextuplet per every possible combination of "integer" angles of the resulting triangle) and I have removed all more or less trivial cases. – user Mar 17 '21 at 13:35
  • 1
    @user Yes, you are right; the combinations of these numbers work. I guess I naturally wanted to group them like this. Let me first try to solve this one geometrically. I am also unsure whether I should update the body of the question, but for now I will work on the problem I have at hand. – krazy-8 Mar 17 '21 at 13:49