7

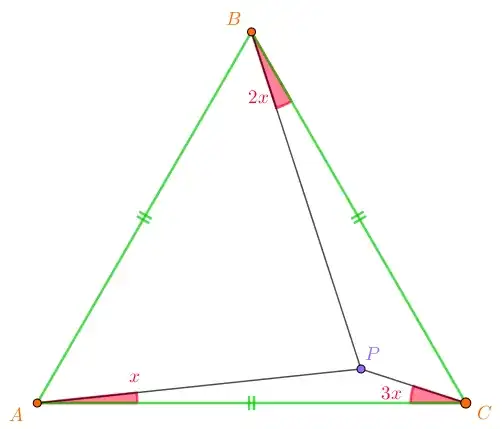
enter image description here

We have a point $P$ inside the equilateral triangle $\triangle ABC$, such that $\angle PAC = x$, $\angle PCA = 3x$ and $\angle PBC = 2x$. Find the value of $x$ in degrees.

I solved the problem in GeoGebra, and I know the value for $x$ is $6°$. Also I solved this problem by using the Trigonometry Ceva's Theorem: $$ \sin(60°-2x)\sin(x)\sin(60°-3x)=\sin(2x)\sin(60°-x)\sin(3x) $$ Where I used WolframAlpha to get $x=6°$.

However, I'm looking for a geometric solution. This is what I have reacher so far. enter image description here

First, draw the circle that lies over $B$, $P$ and $C$. Then extend sides $AB$ and $AC$ to get point $E$ and $D$ (we have another equilateral triangle $\triangle AED$). Due to properties of angles inscribed in a circle $\angle PDC = 2x$ and $\angle PED = 3x$. Then trace the bisector $DG$, we get that $\angle GDP=30°-2x$ and $\angle PGD = 3x$. Here I got stuck. I think, I should proof that $GP = PD$, but I don't know how.

I would appreciate any contribution to this solution, or if you have a different approach and solution I would glad to hear it.

Paúl Aguilar
  • 303
  • 3
    Your GeoGebra skills make me feel woefully inadequate. – saulspatz May 10 '21 at 17:15
  • 1
    Closely related, in particular the second part of second answer: https://math.stackexchange.com/questions/995421/finding-an-angle-between-side-and-a-segment-from-specified-point-inside-an-equil – Intelligenti pauca May 10 '21 at 21:46
  • 1
    Also related: https://math.stackexchange.com/questions/4063800/conjecture-about-a-point-inside-an-equilateral-triangle-divided-by-integer-angle – Intelligenti pauca May 10 '21 at 21:50

2 Answers2

1

enter image description here

Considering figure(left one) in kite ABFC we have:

$\angle BFC+2(\angle ACF)+\angle BAC=(4-2)\times 180=360$

Or:

$(120-2x)+2(\angle ACF)+60=360\rightarrow 180=2(\angle ACF-x)\rightarrow \widehat{ACF}=90+x$

Also in kite ABCG we have:

$(\angle AGC=8x)+60+2(\angle BCG)=360\rightarrow 2(\angle BCG) +8x=300\rightarrow \angle BCG=150-4x$

$BCF-ACF=150-4x-90 -x=60-5x$

$\Rightarrow \angle ACG-\angle BCF=60-5x\Rightarrow 60-5x=ACG-(30+x)$

$\Rightarrow \angle ACG=90-4x$

This equation has following solutions:

$(\angle ACG, x)= (66,6), (70, 5), (74, 4)\cdot\cdot\cdot$

Only $x=6^o$ is competent with equilateral triangle. Figure on the right shows when $x=5$ for example.

sirous
  • 12,694
  • Thank you for the answer. I understood all the steps, however at the end you solve the equation for x = {6°, 5°, 4°, ...}; but how do you realice that 6° is the answer? I didn't get that part, would you give further explaneation please. – Paúl Aguilar May 12 '21 at 18:06
  • In figure on right triangle is isosceles not equilateral. the same is for x=4 and 3. But for x=6 triangle is equilateral which fits the condition in question. – sirous May 13 '21 at 05:00
1

For a geometric solution, make a circle with center $B$ and radius $BA$, thus passing through vertex $C$ of the equilateral triangle.

Let $A$, $D$ be vertices of the regular pentagon in that circle, and $A$, $E$ vertices of the regular decagon. Join $BD$, $BE$. Also join $AD$ and $CE$, intersecting at $P$, and draw $BP$ through to $F$.. Angles inside an equilateral triangle Since $\angle DBC=72-60=12^o$, and $\angle BDG=\frac{180-36}{2}=72^o$, then $BC\perp GD$ and $$\angle PBC=\angle DBC=12^o$$and at the circumference$$\angle PAC=6^o$$And since in the decagon $\angle EBA=36^o$, then at the circumference$$\angle PCA=18^o$$

Hence we have$$\angle PBC=2\angle PAC$$and$$\angle PCA=3\angle PAC$$

Edward Porcella
  • 5,178