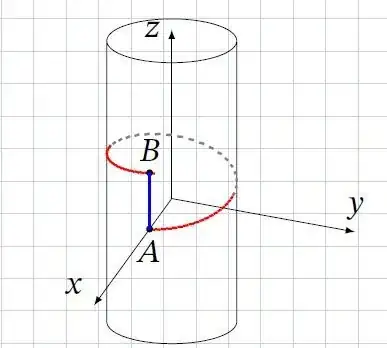
It is known that geodesics on a cylinder are helical lines (helix). As a special case of a helix--- straight line. But one can take two points so cleverly that you can draw two helixes between them (see picture), one of which is a straight line. Both satisfy geodesics differential equation. The question: is, can they both be considered as geodesics or only the shortest one is "true" geodesic?
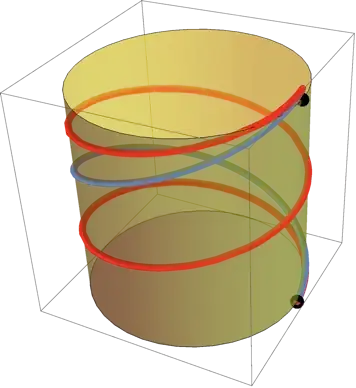
I think the only reasonable definition of a geodesic in such situations involves locally optimal (shorter) paths. After all, consider the case where the two end points are on precisely opposite positions on the cylinder. There are two equivalent arcs (geodesics). (There are an infinite number of geodesics on a sphere linking anti-podes, such as the north and south poles.) For a cylinder there are, then, an infinite number of geodesics in the arbitrary case, indexed by the number of rotations of the helix around the cylinder (like a winding number).
"A geodesic is a locally length-minimizing curve."
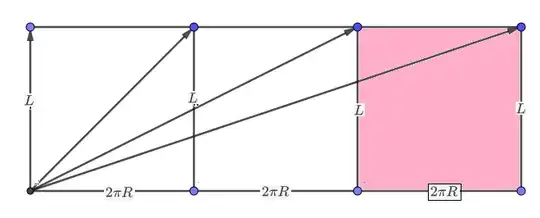
Depending on the number of rotations executed between the end points $(A,B)$ we have an infinite number of local length minimizing geodesics as helices shown on their cylindrical development.
There is one shortest among them running vertically down that you have sketched.
In development all helices are straight lines.
They are inclined to the generator line $L$ as
$$\tan^{-1}\dfrac{n\cdot 2 \pi R}{L}$$
whose periodicity can be visualized as below for $n=0,1,2,3$ in a development of multiple winding numbers associated with periodic wraps.
In your example, both lines are geodesics.
As you correctly state, the general definition of a geodesic is that it satisfies the geodesic equation. But this does neither imply that geodesics are shortest paths nor does it imply that a geodesic connecting two given points has to be unique. Your cylinder is an example showing that both statements can fail. However, there are surfaces where both statements are true, for example the plane. Another example is any region on your cylinder which is simply connected.
Here is a simpler example showing that both statements can fail: Consider a sphere. The equator is a geodesic. Now consider two non-antipodal points on the equator (for example, the most western point and the most eastern point in Africa lying on the equator). There are two geodesics joining those points and only of them is the shortest path. (Note that there are always two possibilities travelling along the equator from point $1$ to point $2$ if the points are distinct.)
Although it is not necessarily true that a geodesic between two points is a shortest path, the converse is true for all surfaces (and more generally, for all Riemannian manifolds): If a constant-speed curve connecting two points is a shortest path between those points, then it is a geodesic. Uniqueness can still fail (consider again the equator but now with to antipodal points).
