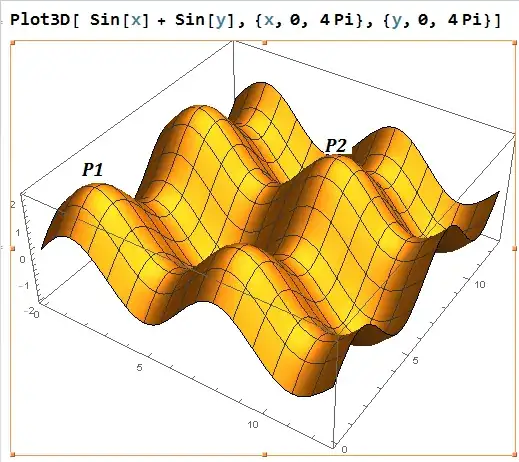
Find all geodesic paths between neighboring peak points P1 and P2 on an egg crate surface of
$$ z= \sin x + \sin y, \; \text{ at}\ (x,y)=(\pi/2,\pi/2), (5 \pi/2), 5 \pi/2)$$
other than the obvious diagonal path connecting them ( through valley /trough bottom ) as intersection with $ x=y $ plane.
In 2D smooth surfaces there is one shortest among many locally geodesic paths(P1-P2)
In case ( think it is unlikely) this path is unique, how is it proved ?