14

I want to strap down a big heavy cylinder on a flatbed truck.

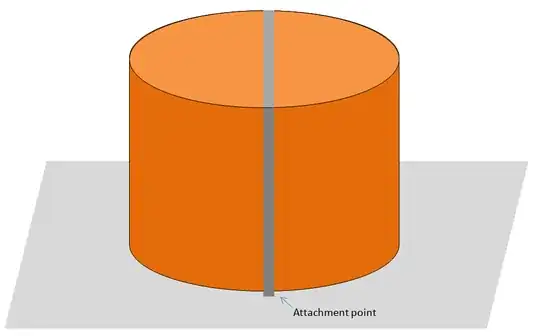
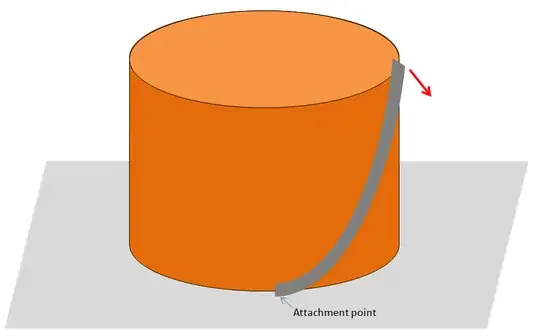
enter image description here

The strap is attached to the truck bed as shown in the picture and also behind.

Will the strap slip off as in the next picture?

enter image description here

PS. This is a purely geometrical question about the length of the strap and the shape of the cylinder. Please consider that the block cannot move sideways and is blocked in place by some metal "foot" at the bottom.

cdupont
  • 265
  • 2
    It looks to me the dangers are the cylinder sliding out from under the strap or the strap breaking. Nothing about the geometry of the cylinder prevents the cylinder sliding sideways; you need at least two straps for that. Whether or not this scheme is safe might depend on 1. The friction between the cylinder end and the truck bed, 2. The expected maximum acceleration "across" the strap, i.e., forward-backward if the strap runs side to side, 3. The strength of the strap and attachment. <> There's probably an engineering site where you can get a more reliable answer. – Andrew D. Hwang Sep 23 '23 at 14:48
  • 3
    @AndrewD.Hwang this is a purely geometrical question about the length of the strap. The cylinder cannot move sideways, I edited the question. – cdupont Sep 23 '23 at 15:05
  • 2
    I'm pretty sure the configuration you sketch uses the minimum length strap, which would answer the geometry question. I could work out the details but won't. You should not think that this strap provides any safety beyond what you have elsewhere. There is serious physics here that the math won't make go away. voting to close. – Ethan Bolker Sep 23 '23 at 15:15
  • @EthanBolker This is a purely geometrical question about the length of the strap. I edited the question to make it more clear. – cdupont Sep 23 '23 at 15:21
  • In any position the strap is able to take you can calculate its length with elementary geometrical methods (assuming its segments are straight). Since you seem to look for a circus horse that jumps over that bar in the arena I won't go into further details. – Kurt G. Sep 23 '23 at 15:32
  • @KurtG. While slipping, the strap sides will not be straight and will need to follow the curvature of the side of the cylinder. The shape of the strap on the slides of the cylinder will probably be portions of an ellipse or portions of an helix. – cdupont Sep 23 '23 at 15:38
  • If you unfold the cylinder it is flat. Hence the strap is? – Kurt G. Sep 23 '23 at 15:40
  • 1
    @AndrewD.Hwang if the cylinder is very flat (e.g. nearly a circle), the strap will not slip. In the case of a circle, the diameter will always be shorter than the semi-circle. However, for very high cylinders, I think it will slip. – cdupont Sep 23 '23 at 15:42
  • Further hints. – Kurt G. Sep 23 '23 at 15:43
  • @KurtG. unfolding the cylinder is a good idea, thanks for the hint. – cdupont Sep 23 '23 at 15:47
  • Now I am going back to my seat in the first row of the circus arena :) – Kurt G. Sep 23 '23 at 15:48
  • This is not a geometry problem because geometry says nothing about tensions in straps or heavy objects. This is a statics problem and may be appropriate for physics.stackexchange. – John Douma Sep 23 '23 at 20:02
  • Incorrect comment deleted; my apology for commenting without first writing out the prospective order-of-magnitude details. – Andrew D. Hwang Sep 23 '23 at 20:07
  • I hope you are not a truck driver! – richard1941 Sep 27 '23 at 02:29
  • @richard1941 ahah no worries, I always drive safely! No more than 6 cement blocks stacked. – cdupont Sep 27 '23 at 07:27

2 Answers2

16

We can model the position of the string as in figure below (where I omitted for clarity the lateral surface of the cylinder): its initial position is along path $ABCD$, but we can study what happens if it follows a slightly displaced path $AEFD$, where $AE$ and $DF$ are geodesic on the cylinder, i.e. straight lines on its unfolding.

If we set $h=AB=CD$, $r=BO=OC$ and $\alpha=\angle BOE$, then the length $l$ of $AEFD$ is: $$ l(\alpha)=2\sqrt{h^2+r^2\alpha^2}+2r\cos\alpha. $$ (Note that $BE=r\alpha$ and that $ABE$ is a right triangle on the unfolded cylinder).

We have $l'(0)=0$ (if $h>0$), but to see if $\alpha=0$ is a point of minimum or maximum, we can compute: $$ l''(0)=2r\left({r\over h}-1\right). $$ Hence $\alpha=0$ corresponds to a minimum only if $r>h$, while for $r<h$ we get a maximum and the string can slip.

enter image description here

Intelligenti pauca
  • 55,765
  • This is fascinating. I tried in my kitchen with various glassware and a bit of string. h=r seems to be the tipping point. – cdupont Sep 23 '23 at 21:44
  • One question, to obtain the last equation did you do the derivation by hand or is there a trick to get it at alpha=0? – cdupont Sep 23 '23 at 21:49
  • I wonder if there is a way to visualize graphically why the tipping point is h=r. – cdupont Sep 23 '23 at 21:51
  • @cdupont I did it by hand and checked it with Mathematica. – Intelligenti pauca Sep 24 '23 at 06:49
  • @cdupont One could explore another model, where $F$ is fixed at $C$ and only point $E$ is displaced. In that case slipping occurs for $h>2r$. – Intelligenti pauca Sep 24 '23 at 06:52
  • Almost, but not quite. Pythagoras is not for triangles with an arc in it. We must have instead $$l(\alpha)=2\sqrt{h^2+4r^2\sin^2(\alpha/2)}+2r\cos\alpha.$$ The end-result is the same, though. Therefore (+1). – Han de Bruijn Sep 27 '23 at 12:45
  • 1
    @HandeBruijn $AE$ is not a straight line but a geodesic (helix) on the lateral surface. Hence I used Pythagoras on the unfolding, because there $AE$ is a straight line. – Intelligenti pauca Sep 27 '23 at 12:47
  • Minor nitpicking, admittedly: your string becomes a bit too long for $\alpha \gg 0$. – Han de Bruijn Sep 27 '23 at 12:58
0

Just to add on @intelligenti's answer. Say that you are pulling the top strap sideways (with both hands) so that it stays parallel to its initial position. As you pull, the top part of the cylinder will "produce" slack because a chord of the circle is always shorter than the diameter. In the same time, the side will "consume" slack because the strap is now oblique instead of vertical. Which one wins?

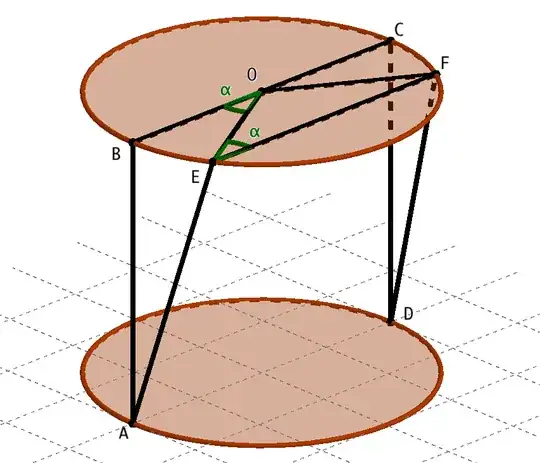
Using the notation of @intelligenti with $r = 1$ and $h = 1$, the top section will produce slack similar to a cosine: $$ 1-\cos\alpha $$ enter image description here

The side will consume slack proportional to: $$ \sqrt {1 + \alpha^2 }-1 $$

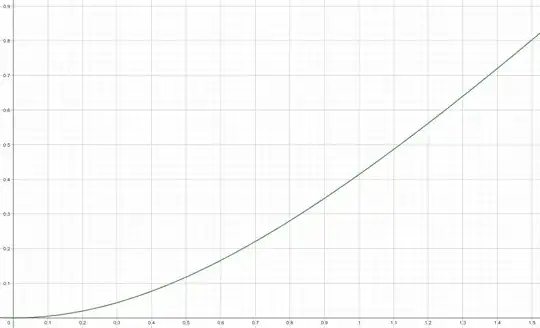
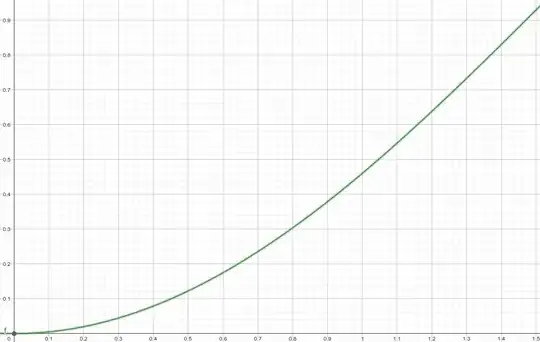
enter image description here

Those two functions looks very similar. Here they are on the same graph.

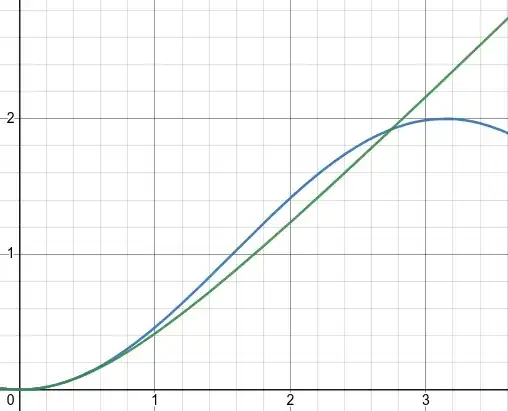
enter image description here

Zooming in, the blue curve is always above the green curve (on the range $0<\alpha<\pi/2)$, so theoretically for $h=r$ it will slip.

Here is a 3D plot with $\alpha$ on the x axis and h on the y axis ($r=1$). Vertically is the amount of slack in total (top - side).

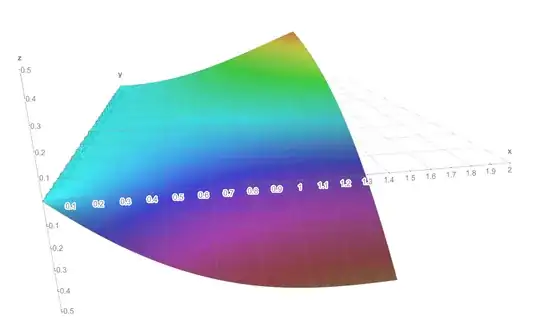
enter image description here

From this plot we can see that for $h<1$, the surface dips below 0 (blue/purple part). More slack is taken than given: it holds tight. For $h>1$, the surface is above 0 (green part): it slips.

Some part of the surface looks funny. Here it is with $h=0.9$ (slightly shorted than the radius):

enter image description here

The curve dips below 0 before getting back up. This shape is normally safe ($h<1$), however if the strap is even slightly elastic or you misplace it, it can reach a point were it will completely slip off.

Shapes below $h=0.74$ are completely safe:

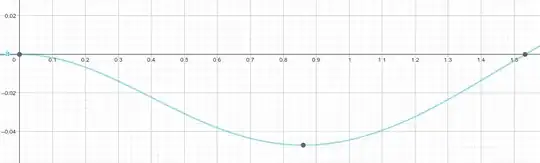
enter image description here

The curve never gets above 0 before $\pi/2$. You can strap them as you want (even close to the border): they will not slip.

cdupont
  • 265