Prove $\left(\frac{2}{5}\right)^{\frac{2}{5}}<\ln{2}$

Question

Inadvertently, I find this interesting inequality. But this problem have nice solution?

prove that $$\ln{2}>(\dfrac{2}{5})^{\frac{2}{5}}$$

This problem have nice solution? Thank you.

ago,I find this $$\ln{2}<\left(\dfrac{1}{2}\right)^{\frac{1}{2}}=\dfrac{\sqrt{2}}{2}$$

following is my some nice methods, use this inequality $$\dfrac{x-y}{\ln{x}-\ln{y}}>\sqrt{xy},x>y$$ then we let $x=2,y=1$

so $$\ln{2}<\dfrac{\sqrt{2}}{2}$$

solution 2:

since $$\dfrac{1}{n+1}\le\dfrac{1}{2}\cdot\dfrac{3}{4}\cdots\dfrac{2n-1}{2n}$$ then $$\ln{2}=\sum_{n=0}^{\infty}\dfrac{1}{(n+1)2^{n+1}}<\sum_{n=0}^{\infty}\dfrac{(2n)!}{(n!)^22^{3n+1}}=\dfrac{1}{\sqrt{2}}$$

solution 3

since $$(1+\sqrt{2})^2(t+1)-(t+1+\sqrt{2})^2=t(1-t)>0$$ so $$\ln{2}=\int_{0}^{1}\dfrac{1}{t+1}dt<\int_{0}^{1}\left(\dfrac{1+\sqrt{2}}{t+1+\sqrt{2}}\right)^2dt=\dfrac{\sqrt{2}}{2}$$ solution 4:

$$\ln{2}=\dfrac{3}{4}-\dfrac{1}{4}\sum_{n=1}^{\infty}\dfrac{1}{n(n+1)(2n+1)}<\dfrac{3}{4}-\dfrac{1}{4}\left(\dfrac{1}{1\times 2\times 3}-\dfrac{1}{2\times 3\times 5}\right)=\dfrac{7}{10}<\dfrac{\sqrt{2}}{2}$$

solution 5 $$\dfrac{1}{\sqrt{2}}-\ln{2}=\sum_{n=1}^{\infty}\dfrac{\sqrt{2}}{(4n^2-1)(17+2\sqrt{2})^n}>0$$

But $$\ln{2}>\left(\dfrac{2}{5}\right)^{\frac{2}{5}}$$ I can't have this nice solution

Thank you everyone can help.

Answer 1

This problem seems to be so hard to prove "elegantly" without aid of calculator, is because you have managed to find such a good approximation! One would need to estimate really well to be able to prove that one is greater than the other.

Continued fractions can be used to give a proof:

$$\left(\dfrac{2}{5}\right)^2 = \dfrac{4}{25} = \cfrac{1}{6 + \cfrac{1}{4}}$$ is a convergent of the the continued fraction of $$(\log 2)^5 = [0; 6, 4, 592, 1, \dots]$$ If you take the CF of $(\log 2)^5$ for granted, the proof of what you want falls right out: $\frac{4}{25}$ is a convergent which is smaller (the convergents alternate bigger/smaller).

Note the apperance of the huge $592$ term, which tells you that $\dfrac{4}{25}$ will be a good approximation, because the convergent corresponding to the $592$ term is greater than $(\log 2)^5$.

Perhaps a more compelling "reason" for it being a good approximation is that the continued fractions of $\log 2 = [0; 1, 2, 3, 1, 6, 3, 1, \dots]$ and $\left(\frac{2}{5}\right)^{2/5} = [0; 1, 2, 3, 1, 6, 3, 2,\dots]$, match up to a good $6$ terms! The $7^{\text{th}}$ term tells you that $\log 2$ must be greater: the parity of the position where two CFs first differ determines if the one with the greater number in that position is greater or not (which also explains the alternating property mentioned above).

If you absolutely want a proof which needs no calculator (i.e. can be verified manually in an hour or so :-)), here is one (with calculations missing):

Take the power series

$$\log (1+x) - \log (1-x) = 2\sum_{n=0}^{\infty} \frac{x^{2n+1}}{2n+1}$$

and set $x = \frac{1}{3}$, you get $\log 2$ on the left.

Now you can truncate the power series at any point, and get a smaller number than $\log (1+x) - \log (1-x)$ , as coefficients are all positive.

Now if you truncate the series at $n=4$ (include $n=4$ term) you get the value $\dfrac{4297606}{6200145}$ which is greater than $\left(\dfrac{2}{5}\right)^{2/5}$. This you can see (manually) by computing the fifth power and computing the (numerator of the) difference of the two fractions you get.

I won't go into more details, as they are quite tedious to do so completely manually without the aid of any calculators, and this is probably not what you were expecting anyway.

Interestingly, it might be easier to do the computations if you work in base $9$ or $3$ (because of the powers of $\frac{1}{3}$, you can quickly read off some of the digits, like spigot algorithms).

Answer 2

$$ \left(2 \over 5\right)^{2/5} = 0.69314\color{#ff0000}{\Large 4}843155146\ldots\,, \qquad\qquad \ln\left(2\right) = 0.69314\color{#ff0000}{\Large 7}180559945\ldots $$

So$\ldots$

Answer 3

Hmm, first I thought the following would allow to compute the proof mentally, but, well... although I find it a remarkable simplification I'll need the pocket calculator in the end. But let's see:

$$\ln(2) \gt (2 / 5)^{2 /5} = \left({16 \over 100 }\right)^{1/5} $$ We have also $$ \ln(2) = \ln \left( 1+1/3 \over 1-1/3 \right) = 2\left( {1\over3} + {1\over 3^3 \cdot 3} + {1 \over 3^5 \cdot 5}+ \cdots \right) \\ = {2 \over 3} \left( 1 + { 1 \over 9\cdot3 } + {1 \over 81 \cdot 5}+ \cdots ) \right) $$ Turn the factor 2/3 to the the rhs then $$ 1 + 1/27 + 1/81/5+ 1/729/7 \cdots \gt \left( {3^5 \over2 \cdot 100 }\right) ^{1/5}= \left( 1+{43\over 200}\right)^{1/5} $$

Now in general we have for a fifth root $$ (1+x)^{1/5} = 1 + x/5 - 2(x/5)^2 + 6(x/5)^3 - 21(x/5)^4 + 399/5 (x/5)^5 - \cdots $$

Thus we must evaluate $$ 1 + 1/27 + 1/81/5+ 1/729/7 \cdots \gt 1 +43/1000 - 2(43/1000)^2 + \cdots $$

"In principle" this can be done with paper & pen only because the terms decrease quickly, and some adaptions of denominators are possible, however, that was too tidy for me. I found using a calculator (Pari/GP) that we must evaluate the lhs with 4 terms and the rhs with 5 terms (of course excluding the 1's) to get the decision - because after that the partial sums in the lhs still increase but in the rhs decrease.

Answer 4

Take $f (x) = \frac {5} {2} \log x + \log 5 - x$. Obviously, $f$ is defined on the interval $]0, \infty[$. Since $f ' (x) = \frac {5} {2x} - 1$, it is easy to see that $f$ increases on $]0, \frac {5} {2}]$, take its maximum at $x = \frac {5} {2}$ and decreases on $[\frac {5} {2}, \infty[$. Also, since $f_{\max} = f (x_{\max}) > 0$ and $f (0+) = f (\infty-) = - \infty$, there are exactly two non-negative real numbers $x_1 < \frac {5} {2}$ and $x_2 > \frac {5} {2}$ such that $f (x_1) = f (x_2) = 0$. Thus, we conclude that $f (x) \geqslant 0$ on $[x_1, x_2]$. Since $x_1 < (2/5)^{2/5} < x_2$, we should have $f \left ((2/5)^{2/5} \right) > 0$, that is, $$\log 2 - (2/5)^{2/5} >0,$$ as desired.

Answer 5

Your question is interesting, but it boils down to the property of $x^x$.

You can derive from your inequality an implicit form $y^x \ln^y(x)-x^x$, $y=5$, $x=2$ and simply try to solve by $y$ this equality, $y^x\ln^y(x)-x^x=0$

This equation surprisingly has a closed form solution $y=\frac{x\,W(\ln(\ln(x)))}{\ln(\ln(x))}$ where $W$ is Lambert function, an inversion of $We^W=z$. Now simply:

$$\frac{W(\ln(\ln(2)))}{\ln(\ln(2))} \approx 2.4997... < \frac{5}{2}$$

This is the reason for your inequality.

On the other hand the solution of

$$\frac{W(\ln(\ln(x)))}{\ln(\ln(x))} = \frac{5}{2}$$ is $x=e^{(\frac{2}{5})^\frac{2}{5}} \approx 1.999 < 2$ again fits your inequality

From here you can see that any proof is nothing more than computation exercise and probably the simplest one is to take first few digits of $\ln(2)$ and raise it to fifth power. Lambert function is an object of its own, and if you attach it to something like $\ln(\ln(2))$ you have to expect employing some highly precise technique.

This is the entire and the shortest proof:

$$ (ln(2) \cdot 10^6)^5 > 693145^5=160000181024126357095762965625>0.16 \cdot 10^{30} = (\frac{2}{5})^2 \cdot 10^{30}$$

Interesting part is to explain the reason we have so close match in the first place. One of the interesting equivalent forms is $f(x)=e^{(\frac{1}{x})^\frac{1}{x}}-2$ We want to know what is happening around $f(\frac{5}{2})$

$f(x)=e^{(\frac{1}{x})^\frac{1}{x}}-2$ has the minimum at $e^{(1/e)^{1/e}}-2$ at $x=e$. One of the two zeros is at $x=\frac{W(\ln(\ln(2)))}{\ln(\ln(2))}$ which means $f(\frac{5}{2})<0$

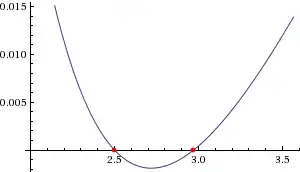
Still, this does not explain the closeness of the zero itself to 2.5. Let us look back to $y=\frac{x\,W(\ln(\ln(x)))}{\ln(\ln(x))}$

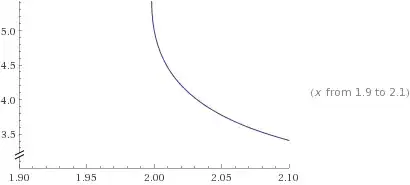
The reason the point $x=2,y=5$ is so close to the curve $y=\frac{x\,W(\ln(\ln(x)))}{\ln(\ln(x))}$ is that the function is almost vertical around 2.

After some not so difficult calculations you can find that the first derivative of $y=\frac{x\,W(\ln(\ln(x)))}{\ln(\ln(x))}$ has one of the factors as $\frac{1}{W(\ln(\ln(x))) + 1}$ and this is the key point since $W(\ln(\ln(x)))=-1$ has the solution $x=e^{(1/e)^{1/e}}$ which is as we have shown smaller than but very close to 2.

We have $y(e^{(1/e)^{1/e}})=e \cdot e^{(1/e)^{1/e}} \approx 5.43...$ Since the function is almost vertical around 2, this means that moving from 5.43 to 5 we would still remain close to 2.

In essence, a really technically complete proof requires to find a good estimation for

$$\frac{e \cdot e^{(\frac{1}{e})^{\frac{1}{e}} }-5}{2-e^{(\frac{1}{e})^{\frac{1}{e}}}}$$

and to prove that this is larger than the average slope for $y=\frac{x\,W(\ln(\ln(x)))}{\ln(\ln(x))}$ in the interesting region. This would mean that we could not reach 2 going from $e^{(1/e)^{1/e}}$ down the slope.

However, this or any similar method would require the precision that is definitely higher than purely calculating six-digit fifth power, but it is interesting to reveal the magic behind the inequality nevertheless.

Answer 6

There is a remarkable series converging to $\ln(2)$ on Wikipedia: $$\ln(2)=\sum_{k=0}^\infty\frac{2}{2k+1}\left(\frac{7}{31^{2k+1}}+\frac{3}{161^{2k+1}}+\frac{5}{49^{2k+1}}\right)$$ although I don't see a source for why this is true.

Summing just the $k=0$ and $k=1$ terms, gives $$\begin{align} \ln(2)&>\frac{29558488681560}{42643891494953}\\ \ln(2)&>0.693147\\ \left(\ln(2)\right)^5&>(0.693147)^5\\ \left(\ln(2)\right)^5&>0.160002\\ \left(\ln(2)\right)^5&>\frac{4}{25}\\ \ln(2)&>\left(\frac{2}{5}\right)^{2/5}\\ \end{align}$$

Answer 7

Using the Taylor series $$\ln \frac{1+x}{1-x} = \ln (1 + x) - \ln(1 - x) = 2\sum_{k=0}^\infty \frac{x^{2k+1}}{2k+1}, \quad -1 < x < 1;$$ letting $x = 1/3$, we have $$\ln 2 = 2\sum_{k=0}^\infty \frac{1}{3^{2k+1}(2k+1)}. \tag{1}$$

Using Bernoulli inequality, we have, for all $a > 0$, $$(2/5)^{2/5} = \frac{1}{a^2}\left(\frac{2}{5}a^5\right)^{2/5} \le \frac{1}{a^2}\left(1 + \left(\frac{2}{5}a^5 - 1\right)\cdot \frac25\right) = \frac{4}{25}a^3 + \frac{3}{5a^2}$$ with equality if and only if $a^5 = \frac52$.

It suffices to prove that, there exists $a > 0$ such that $$\frac{4}{25}a^3 + \frac{3}{5a^2} < \ln 2.$$ When $a^5 \approx \frac 52$, from $\frac{4}{25}a^3 + \frac{3}{5a^2} = \frac{4a^5}{25a^2} + \frac{3}{5a^2} \approx \frac{4\cdot (5/2)}{25a^2} + \frac{3}{5a^2} \approx \ln 2$, we have $a^2 \approx \frac{1}{\ln 2} \approx \frac{81}{56} = 1.4464$ and $a \approx 1.2$ where we have used (1) to get $\ln 2 \approx 2\sum_{k=0}^1 \frac{1}{3^{2k+1}(2k+1)} = \frac{56}{81}$. Letting $a = \frac{6}{5}$, it suffices to prove that $$\frac{4}{25}(6/5)^3 + \frac{3}{5(6/5)^2} < \ln 2.$$ Using (1), we have $$\ln 2 > 2\sum_{k=0}^5 \frac{1}{3^{2k+1}(2k+1)} = \frac{15757912}{22733865}.$$ It suffices to prove that $$\frac{4}{25}(6/5)^3 + \frac{3}{5(6/5)^2} < \frac{15757912}{22733865}$$ which is true.

We are done.

Answer 8

The Newton-Raphson method for $x=\left(\frac{2}{5}\right)^{2/5}$ is $x_{n+1}=\frac45x_n+\frac{4}{125x_n^4}$. Take $x_0=1$ and assume that each $x_n\geq\left(\frac{2}{5}\right)^{2/5}$. Compute the iterations up to $x_5=0.693145$, using a sufficient level of precision, around $6$ decimals. Finally, compute the upper bound of $e^{x_5}$ with the first $8$ terms of its Taylor series plus another $8$th term.

$$1.999997=\sum_{n=0}^8\frac{(x_5)^n}{n!}+\frac{(x_5)^8}{8!}\geq e^{x_5}\geq e^{\left[\left(\frac25\right)^{2/5}\right]}$$

Therefore, $\ln(2)\geq\left(\frac25\right)^{2/5}$. The exercise is a question of how few arithmetic operations you need to reach the inequality. This method has a total of $36$ multiplications, $16$ divisions and $14$ additions *, which is feasible to do within an hour or so, despite being rather tedious.

---

* Each Newton-Raphson iteration takes $5$ multiplications, $2$ divisions and $1$ addition. For $n>0$, each term in the series takes at most $2$ multiplications, assuming the previous power of $x_5$ and factorial were stored. Each term also requires $1$ division and $1$ addition. The $n=0$ and repeated $n=8$ terms of the series are single additions.