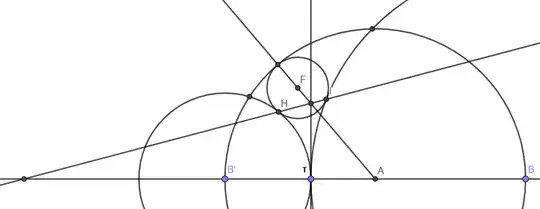
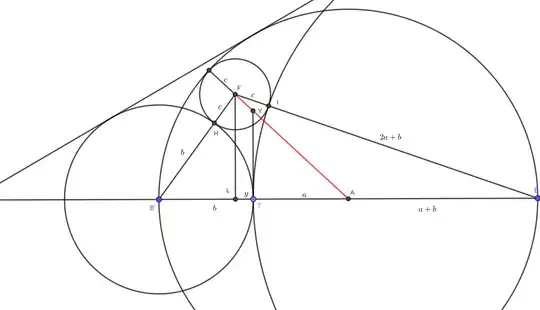
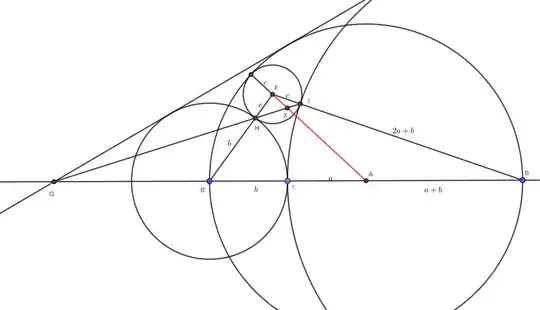
$c_1$ centered at $A$ passing through $B$.
$BB′$ is a diameter of $c_1$.
$T$ a random point in segment $BB′$.
$c_2$ centered at $B′$ passing through $T$.
$c_3$ centered at $B$ passing through $T$.
$c_4$ tangent externally to $c_2$ and $c_3$ and internally tangent to $c_1$
$F$ is center of $c_4$ and $H,I$ are tangency points.
It is clear to me that $Z = HI \cap AF$ is the second homothety center of $c_1$ and $c_4$ and I would like to prove that it also lies in that line perpendicular to $AB$ through $T$.
important related result that you probably should know: Show these three circles share their external common tangent lines
This seems to be a general result about soddy circles