1

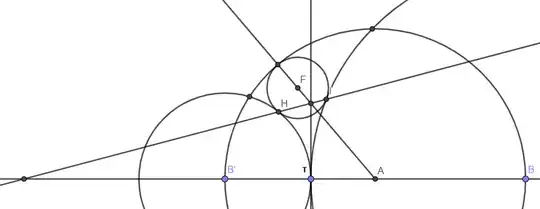
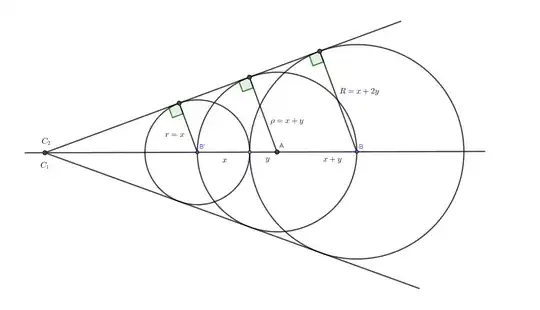
it is a silly problem but I would like to see some ways to show that the external tangent lines from $c_1$ and $c_3$ are also the external tangent lines from $c_1$ and $c_2$:

$c_1$ centered at $A$ passing through $B$.

$BB'$ is a diameter of $c_1$.

$T$ a random point in segment $BB'$.

$c_2$ centered at $B'$ passing through $T$.

$c_3$ centered at $B$ passing through $T$.

enter image description here

To show that $c_1,c_2,c_3$ are all tangent to two lines whose bissector is the support line of $AB$ (who meet in $HI \cap AB$ in the image above).

nonuser
  • 91,557
hellofriends
  • 2,048
  • 1
    If you just want to show that the three circles have a common tangent line, a key observation is that the perpendicular at $T$ bisects the common external tangent segment of $\bigcirc B$ and $\bigcirc B'$. From this, one can show that the bisection point is in fact the point of tangency of common tangent line with $\bigcirc A$. ... Showing the involvement of $\overleftrightarrow{HI}$ is more work. – Blue Aug 05 '20 at 17:37
  • oh I don't need the $HI$ line, thanks @Blue. I was looking for a short synthetic way to see what you pointed. – hellofriends Aug 05 '20 at 17:57
  • @Blue wait is this part obvious: "From this, one can show that the bisection point is in fact the point of tangency of common tangent line with ◯A" ? – hellofriends Aug 05 '20 at 18:00
  • 1
    ok I think i got it. The distance between the contact points is $2\sqrt{Rr}$ the mid point is $\sqrt{Rr}$ which is the height of the right triangle formed by the perpendicular line through $T$. This means the midpoint is also that meeting of the line. – hellofriends Aug 05 '20 at 18:14
  • That's how I did it. :) – Blue Aug 06 '20 at 00:43
  • is that archemedes circle – endgame yourgame Aug 06 '20 at 06:38
  • i think archemedes circle would have BT as diameter instead of radii – hellofriends Aug 06 '20 at 10:48

1 Answers1

2
  • We need a following boxed lemma. Let $C$ be a center of homothety which takes one circle to second.

Because of triangle similarity we have $${CO'\over CO} ={R\over r}\implies \boxed{CO = OO'{r\over R-r}}$$

enter image description here

  • Back to the problem. enter image description here

Let $C_1$ be a center oh homothety which takes $c_2$ to $c_1$ and let $C_2$ be a center oh homothety which takes $c_2$ to $c_3$. All you need to prove is $C_1=C_2$ using boxed formula.

nonuser
  • 91,557