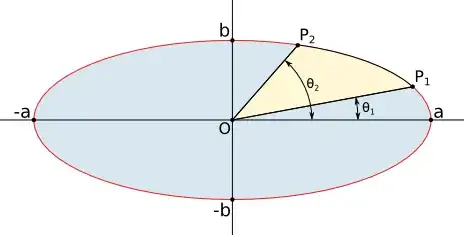
I'm trying to calculate the length of an elliptical arc using Excel and later C++.
The range is not $[0, \pi/2]$, and not $[0, \pi]$, and not $[0 ,2\pi]$, but $[0, \pi/3]$.
Nowhere can I find a clear explanation of a way to calculate this. Not even an infinite series using two angles as arguments. Everywhere the question is answered by giving the circumference or $1/2$ or $1/4$ of it, not the arc length as defined by an argument.
I'd just like to find an expansion with which I can find a numerical solution to the incomplete elliptic integral of the second kind, a series which doesn't contain 'new' functions e.g. gamma, K(), B(), C(), D(), etc.
Thank you.