2

Hope you are well and safe

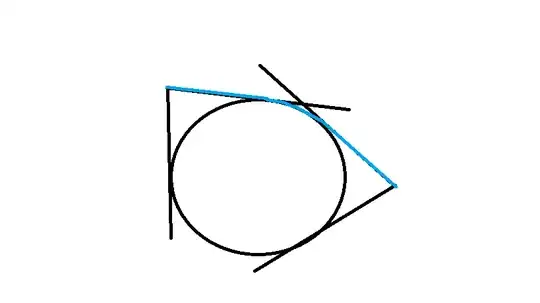
The following question is to find the shortest distance between 2 points avoiding a circle between them using the Maximum principle (see photo 1 & photo 2).

the solutions are divided into 3 cases, before the obstacle (the circle), touching the circle and finally leaving the circle.

Our Hamiltonian Equation is $H(x,p,a) = p(a) -1 = p^1a^1 + p^2a^2 -1$ and that because we are is $R^2$ , all and our dynamic is $x` = a$. all of these detail are shown in photo 2.

in photo 2: the showed the case 1 (before the obstacle) and they started with case 2.

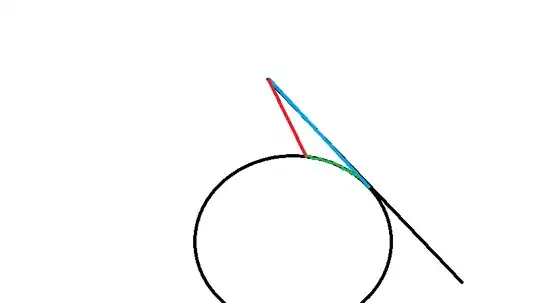
My problem is in case 2: I was able to get all the 5 equations he mentioned, but at end of the page he says: "we introduce the angle theta as illustrated (in photo 4), and note that $\frac{d}{d \theta} = r \frac{d}{dt}$. A calculation then confirms that the solutions are...". The obtained solutions at the end of photo 3 are wrong, and I tried to get them right but I couldn`t.

MY Goal: I need the calculations to get the right solutions for the 5 unknows (the red box in photo 3). it is an algebra problem more than a concept of optimal control theory. if you have any intuition or suggestion please tell me.

photo 1: https://i.sstatic.net/BkGwn.jpg

photo 2:https://i.sstatic.net/jeeiq.jpg

photo 3:https://i.sstatic.net/yBJtK.jpg

photo 4:https://i.sstatic.net/nPxVd.jpg

Viktor Vaughn
  • 20,897
Twitch Gaming Clips
  • 41

1 Answers1

0

If the line connecting the two points passes through the circle, then the shortest path avoiding the circle will look like the blue path in this image:enter image description here

Can you see why the shortest path can only contain straight lines and arcs of the circle? Hint: if the path contains a curved line which is not bordering the circle, you can tweak it into a shorter path.

To see why the shortest path connects the points to the circle using tangent lines, look at the image below. The path along the blue line is shorter than the path along the red line and green arc. enter image description here

Angela Pretorius
  • 10,280
  • from case 1 (before touching the circle) we have proved that it is a straight line. But how would I show it a straight line using the equations I have or using the angle theta (which the angle created by hitting the circle and go out from it )? thank you – Twitch Gaming Clips Apr 03 '20 at 22:04
  • @TwitchGamingClips Are you asking for a proof that the shortest distance between two points is a straight line? What are $x,p,a$? Are you trying to maximise the Hamiltonian of a particle which travels from the first point to the second and has position $x(t)$ at time $t$? – Angela Pretorius Apr 04 '20 at 06:49
  • I am trying to maximize the payoff function that is mentioned in photo 2. I am not asking for proof that the shortest between 2 points is a straight line. My question is: how to get the unknows (in the red box)? using the 5 equations – Twitch Gaming Clips Apr 04 '20 at 11:18