Proof of shortest path avoiding ball

Question

I have read in a number of places that the shortest path between two points $a,b\in \mathbb{R}^2$ that avoids a disk $D$ between them (by "between" I mean the disk intersects the line $a-b$) is of the form: travel along a tangent line to $D$ that intersects $a$, then travel in a circle arc along $D$, then travel along the tangent line to $D$ that intersects $b$. (Picture below)

Is there a standard proof of this fact? It seems almost obvious if you consider the physical problem of pulling a rope, lain over a circular pully, taut. However, I haven't been able to prove it. The only other post I could find discussing this problem seems to suggest that optimal control theory could be used to solve it, though I wonder if even that is overkill. Any insights or references would be appreciated.

Answer 1

This fact quickly becomes clear if you draw the tangent lines from $a$ and $b$ to $D$, and consider the (open) regions bounded by these tangent lines and $D$:

Suppose that a shortest path from $a$ to $b$ that avoids (the interior of) $D$ passes through one of the four regions $Ai$, which do not include their boundaries (the tangent lines):

• If the shortest path passes through region $A2$, then it must also exit region $A2$ by meeting either tangent line $L_1$ or tangent line $L_2$. Then this part of the path is a shortest path between to points on a (tangent) line, hence it is a segment of that tangent line. But then it does not pass through region $A2$, a contradiction.

• If the shortest path passes through $A1$ or $A4$ then it must cross the tangent line $L_1$ to $D$ at another point. Then this part of the path is a shortest path between to points on a (tangent) line, hence it is a segment of that tangent line. But then it does not pass through regions $A1$ or $A4$, a contradiction.

• Similarly, if it passes through $A3$ or $A4$ then it must cross the tangent line $L_2$ to $D$ at another point. Then this part of the path is a shortest path between to points on a (tangent) line, hence it is a segment of that tangent line. But then it does not pass through regions $A3$ or $A4$, a contradiction.

This shows that the shortest path does not enter any of the regions $Ai$, and so it starts with a line segment $a-a_i$. By symmetry, it ends with a line segment $b_i-b$.

Of course the shortest path between two points on the boundary of $D$, that avoids the interior of $D$, is the (short) circular arc between these two points. This follows straightforwardly from the triangle inequality.

Answer 2

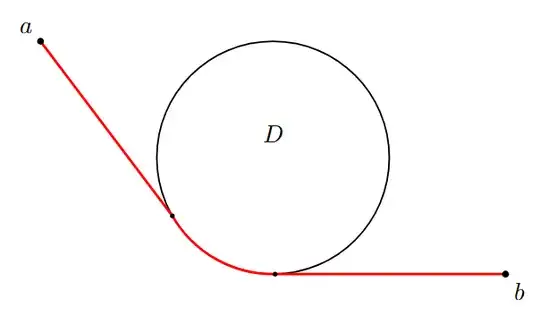
Your idea of the rope spanned over a circle is the right way of atacking such problems. The method is called Euler-Lagrangian equations of motion with undetermined parameters simulating the boundary of a free particle taking the shortest path between two points; avoiding an area with such a high potential (a high mountain with steep flanks), that would be slowing down the velocity, such that any path circumventing the area is cheaper wrt to kinetic energy and shorter wrt to travel time.

Lagranges method of undetermined free parameters is using an arbitrary high potential energy inside the forbidden area resulting in a very hard, potentially infinite, elastic repulsion forces acting orthogonal to the tangent of the boundary, such that the boundary causes a momentum reflection if the path touches the boundary.

Without much mathematical ado it easy to show that the shortest path is a series of straight lines and pieces of the boundary, that between first and last touch of the boundary forms a convex hull og its inner segment between the two touching points.

For a segment of the circle the convex hull is the segment itself.

If there are defects or inward curved parts of the segment, they are bridged by shortest straight thangents.

In a way this is old roman art of road construction, were the number of stones and brigdes on the on hand and the travel tíme and coast on the other hand were the variation principles for the engineers to find the optimal route.

As a mathematical profund description the method needs so much of calculus of variation and differential geometry, that it fills about half of any textbook of theoretical mechanics.