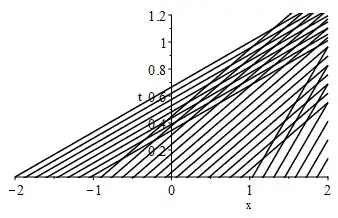
I'm trying to plot the characteristics for the following PDE with initial conditions:
$$u_t +uu_x =0$$ where $$u(x,0)= \begin{cases} a \quad \text{for}\quad x<-1,\\ b \quad \text{for}\quad {-1}<x<1,\\ c \quad \text{for}\quad x>1. \end{cases}$$
I'm first trying to plot for the case where $a>b>c$. I understand what the plot should look like, however, I've so far been unable to produce it in MAPLE. Does anyone have any help to do this?