Quasilinear PDE with ambiguous quadratic equation solution

Question

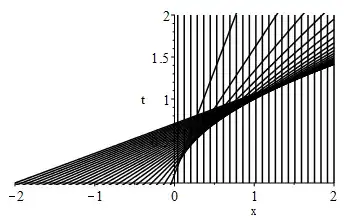
Suppose we have

$$u_t + [u^2]_x = 0,~~~~u(x,0) = \begin{cases} \sqrt{-x}, &x < 0 \\\\ 0, &x > 0 \end{cases} $$ and we want to find some solution utilizing shocks and entropy conditions.

Attempt:

Solving by the Method of Characteristics gives the implicit solution $u(x,t) = g(x - 2ut)$, for some $g$. If we parameterize by $s$ we can get characteristics of form $x = 2tg(s) + s$. Then, for $s > 0$, we clearly see

$$u(x,t) = 0, ~~~~ x > 0,$$

but for $s < 0$, we look at $g(s) = \sqrt{-s}$. So,

$$ x = 2t\sqrt{-s} + s \Rightarrow s^2 + (4t^2 - 2x)s + x^2 = 0,$$

which is a quadratic equation. Solving this gives

$$s = x - 2t^2 \pm 2t\sqrt{t^2 - x},$$

and so we have

$$u(x,t) = \sqrt{2t^2 - x \pm 2t\sqrt{t^2 - x}}, ~~~~ x - 2t^2 \pm 2t\sqrt{t^2 - x} < 0.$$

I'm struggling with how to interpret this since we have a "$\pm$". Do we treat these as two separate equations, and then check for shocks that way?

Answer 1

To gain insight into the problem, let us plot the base characteristics curves $x = 2tg(s) + s$ deduced from the method of characteristics for several values of $s$:

Solving $x = 2 t \sqrt{-s} + s$ for $s<0$, we find the two families $$ s = x-2t^2 \pm 2t\sqrt{t^2 - x} \, ,\qquad u = \sqrt{2t^2 - x \mp 2t\sqrt{t^2 - x} } $$ valid for $x<t^2$. These two families correspond to lines that intersect in the figure. Note that the characteristic curves should be stopped once they have intersected, as the method of characteristics becomes obsolete. Here are some ways to choose the correct family of curves:

• Graphically: by stopping the curves at the smallest positive time where they intersect another one, we are able to choose the correct family. For instance, setting $(x,t) = (0,0.5)$ leads to $s = -0.5\pm 0.5$, which suggests that the expressions with the bottom sign are the correct ones.

• Initial conditions: here, both solutions issued from the method of characteristics satisfy $u = \sqrt{-x}$ at $t=0$, thus we won't learn anything from the initial condition (see e.g. this related post where it works). To overcome this issue, let us evaluate the partial derivatives of $u$, and then $$ \left.\frac{u_t}{u_x}\right|_{t=0} = \pm 2\sqrt{-x} \, . $$ Since the above quantity must equal $-2u|_{t=0}$, we conclude that the expressions with the bottom sign are the correct ones.

Note that the characteristic curves issued from negative $s$ intersect with those issued from positive $s$. Thus, the Rankine-Hugoniot condition will be required to compute the discontinuity that emanates from this interaction (cf. this post).