2

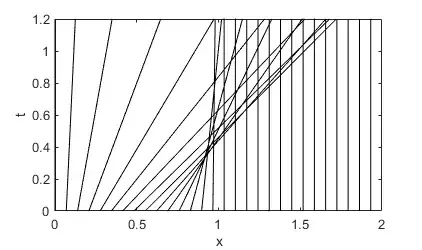
I'm trying to plot the characteristics for the following problem.

Consider the first order nonlinear hyperbolic PDE (the inviscid Burgers' equation) $$ \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} = 0 , \tag{1.2a} $$ with the boundary and initial conditions defined by $$ u(0,t) = 0,\qquad u(x,0) = \begin{cases} \sin^2(\pi x) &\quad 0\leq x\leq1,\\ 0 &\quad 1\leq x\leq 2. \end{cases} \tag{1.2b} $$

So far I have managed to find all the gradients for the lines from each value of $x_0$. But I'm not sure how to plot it. It seems like a very simple question but one I'm finding really difficult. I also cannot use any inbuilt matlab functions except the very minimal ones such as plot.

Here is my code so far..

dx=0.01;%spatial step
dt=dx;%set time and space steps equal
X=2;%end of space interval
x=0:dx:X;%space vector formed
Tf=1;%end of time interval
n=floor(X/dx);%number of overall space steps
n1=floor(1/dx);%number of space steps needed - 1st interval
timesteps=floor(Tf/dt);%number of time steps

u1=sin(pix).sin(pi*x);
u11=u1(1:n1);
u2=zeros(1,n1+1);


%initial conditions


u0=[u11,u2]; %form ic vector u0
u=u0;
c=1./u0;%gives the gradients of each x0 point
EditPiAf
  • 21,328
f_olivere
  • 49

1 Answers1

1

In the present case, the method of characteristics leads to the characteristic curves $$ x = x_0 + \phi(x_0) t , \qquad 0\leq x_0\leq 2 , $$ where $\phi = u(\cdot,0)$ is the initial data. Along these curves, we have $u = \phi(x_0)$. Let us plot those curves for several values of $x_0$:

phi = @(x) (x<1).*sin(pi*x).^2;
[xmin,xmax,tmax,n] = deal(0, 2, 1.2, 30);
x0 = linspace(xmin,xmax,n);
x = linspace(xmin,xmax,200);
for i = 1:n
  plot(x, (x-x0(i))/(phi(x0(i))+eps), 'k-');
  hold on
end
ylim([0,tmax]);
xlabel('x');
ylabel('t');

Output:

characteristic curves

See also the Maple version in this post.

EditPiAf
  • 21,328