-1

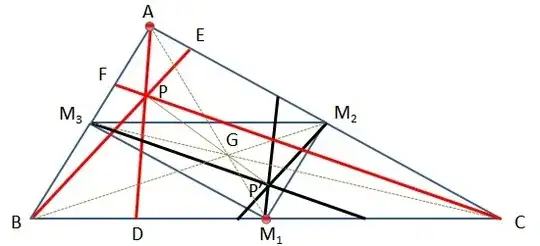
$AD$, $BE$ and $CF$ are concurrent lines on $\triangle ABC$. Show that lines through the midpoints of $BC$, $CA$ and $AB$ respectively parallel to $AD$, $BE$ and $CF$ are concurrent.

Let $M_1$, $M_2$ and $M_3$ be midpoints of $BC$, $AC$ and $AB$ respectively. Lines parallel to $AD$ and $BE$ pass through $M_1$ and $M_2$ respectively meet at point $O$. It suffices to prove that line from $M_3$ to $O$ is parallel to $CF$.

I am guessing that this has to do with Ceva's theorem. But I am unable to use it to prove the statement. It is really confusing because of so many lines in the figure. Kindly post your solutions.

enter image description here

Mohsen Shahriari
  • 7,071
Mathematical Curiosity
  • 1,035

2 Answers2

1

The original triangle $ABC$ and its medial triangle $M_1 M_2 M_3$ are related via a dilation $\delta$ centered at the common centroid $G$. Any dilation preserves parallel lines and concurrency, so if $AD,BE,CF$ are concurrent so they are their images via $\delta$, i.e. the given lines through $M_1,M_2,M_3$.

Jack D'Aurizio
  • 361,689
1

I just saw that the same question has been asked on some days before here with an answer using Ceva's theorem.

What follows is not an answer. Just a comment and a figure on which the excellent proof by Jack D'Aurizio can be better understood.

Comment : Maybe, you haven't much done transformation geometry, in particular with dilations (also called homotheties) like δ (as named in the solution above) with a negative ratio −1/2 as mentionned for example here. Begin by understanding what a dilation with ratio $r>1$ means and why images of lines transported are parallel line (a property shared by all affine mappings if you happen to know this name).

Figure :

enter image description here

Jean Marie
  • 88,997
  • The correspondence $P \leftrightarrow P'$ has as a particular case : $I (incenter) \leftrightarrow S (Spieker \ center) \ X(10)$ See here. – Jean Marie Jul 10 '24 at 13:50