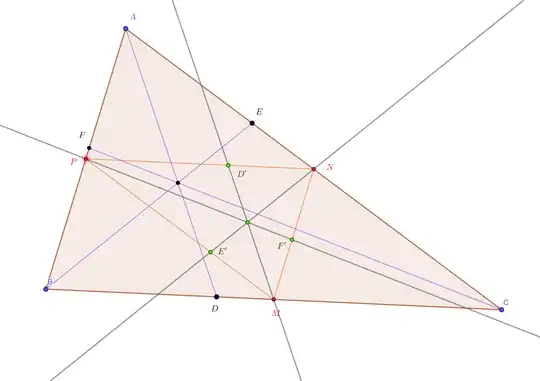
$AD$, $BE$, $CF$ are concurrent in $\triangle ABC$. Show that lines through midpoints of $BC$, $CA$, $AB$ parallel to $AD$, $BE$, $CF$ are concurrent.

Question

$AD$, $BE$, $CF$ are concurrent lines in $\triangle ABC$. Show that the lines through the midpoints of $BC$, $CA$, $AB$ respectively parallel to $AD$, $BE$, $CF$ are concurrent.

My attempt

I tried using Ceva's theorem but not getting how to use it. Please give me a hint.

I know this question has already been answered (for instance, see here), but I want hint related to Ceva's or Menelaus' theorem.

Answer 1

Let $\Delta ABC$ be a triangle, denote by $M,N,P$ the mid points of the sides opposite to $A,B,C$. Let $D$ be a point on $BC$. The parallel to $AD$ through $M$ intersects $NP$ in a point denoted by $D'$.

Construct $E',F'$ in a similar way on the sides of $\Delta MNP$.

Because $MN$, $ND'$, $D'M$ are parallel to (respectively) $AB$, $BD$, $DA$, we obtain a triangle similarity, so $D'N:DB=MN:AB=1:2$. This gives $D'N:D'P=DB:DC$.

We finally apply Ceva (and the reciprocal) in the two triangles $\Delta ABC$, $\Delta MNP$: $$ \frac{D'N}{D'P}\cdot \frac{E'P}{E'M}\cdot \frac{F'M}{F'N} = \frac{DB}{DC}\cdot \frac{EC}{EA}\cdot \frac{FA}{FB} = -1\ . $$ $\square$

---

Later edit: Quick picture inserted: