How to interpret clusters on Markov chain time characteristics?

Question

I have a complex network $G=(V,E)$ from multivariate financial time series in which a single vertex $v_i$ represents the types of states corresponding to the combination of the fluctuations of the prices on a given time frame, a single edge $(v_i,v_j)$ denotes the transition from node $v_i$ to node $v_j$.

Then, I associated the graph $G$ with a first-order discrete-time Markov Chain as follows. The node set $$V(G)= \{v_1, v_2, \ldots, v_n\}$$ is the finite discrete state space and the edge set $$E(G) \subseteq V(G) \times V(G)$$ determined by the rule $e=(v_i, v_j) \in E(G)$ for $v_i, v_j \in V(G)$, corresponds to states’ transitions, and the edge weight is the transition probability between two states $v_i$ and $v_j$.

I have computed the eigenvalues of the transition matrix. All eigenvalues ​​lie in a unit circle (except 1) and the spectral gap equals $1- |\lambda_2|=0.38$. The Markov chain is aperiodic (because self-loops exist) and is irreducible.

I have found the mean recurrence time (left graph) and then sorted mean recurrence time (right graph). 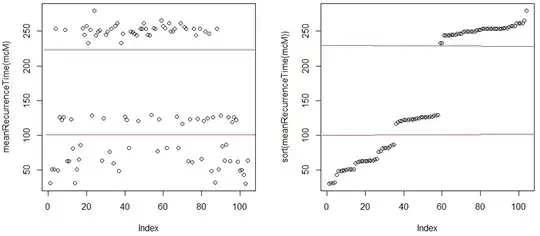As on the left graph as on the right graph, one can see three 'clusters' (sets). I think that is not a typical case. Maybe the transition matrix has a specific form?

My question is: How to interpret obtained clusters (subgraphs) for Markov chain time characteristics? I am looking for a possible practical interpretation.

Edit 1.

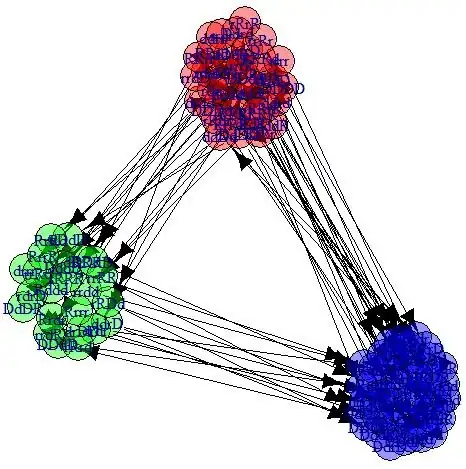
I have plotted the original graph $G$ with tree 'clusters'. Then densities, diameters for subgraphs were calculated.

  cluster vertexN edgeN     density diameter
       1      35   105  0.088235294  1.30119
       2      23    12  0.023715415  1.00000
       3      46    10  0.004830918  2.00000

Density of original graph is 0.0229649.

Refs

Meyn S P and Tweedie R L 2005 Markov Chains and Stochastic Stability

Zhang N. Prediction of financial time series with hidden markov models: Shandong university, China, 2001

Answer 1

Spectral methods for clustering are all based on the idea of using the spectral properties of Markov chains subsumed by a given problem. There are a number of works that used the idea you mentioned in your post for clustering purposes. All those works transform the input into a Markov chain, and then find sets of states in the Markov chain in which the mean residence time as well as the mean time between sets are both large.

The Google Page rank algorithm is a ranking algorithm based on the abstraction of a random surfer -- i.e., a random walker. In essence, the same abstraction can be used for clustering purposes. So, ultimately the Google Page rank is also a spectral method, used for ranking rather than clustering.

The connection between random walks and clustering is clearly described in this paper here:

AVRACHENKOV, Konstantin; EL CHAMIE, Mahmoud; NEGLIA, Giovanni. Graph clustering based on mixing time of random walks. In: 2014 IEEE International Conference on Communications (ICC). IEEE, 2014. p. 4089-4094.

AVRACHENKOV, Konstantin et al. Pagerank based clustering of hypertext document collections. In: Proceedings of the 31st annual international ACM SIGIR conference on Research and development in information retrieval. 2008. p. 873-874.

section 6 fo the following paper is also very helpful

Von Luxburg, U. (2007). A tutorial on spectral clustering. Statistics and computing, 17(4), 395-416.

https://link.springer.com/content/pdf/10.1007/s11222-007-9033-z.pdf