I find many sites explaining how to use Newton's method, but none explaining why it works. Could someone give me the intuition behind it? Thanks.
- 76,540
- 435
- 1
- 4
- 5
-
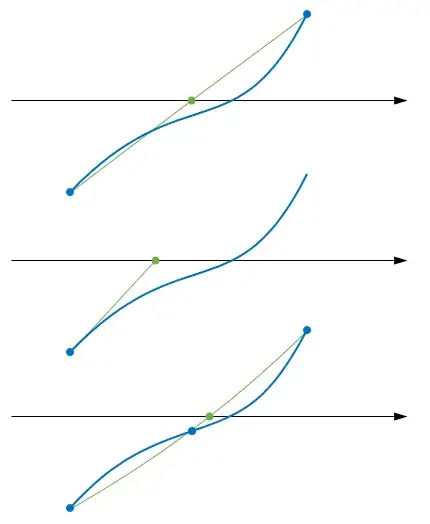
2Somebody must have provided a picture. Let $x_n$ be our current estimate. Then the next estimate $x_{n+1}$ is obtained as follows. Draw the tangent line at $(x_n, f(x_n))$. Then $x_{n+1}$ is the point where the tangent line meets the $x$-axis. Draw a smooth curve that crosses the $x$-axis at $r$. Let $x_n$ be close to $r$. Draw the tangent line described above. It meets the $x$-axis at a point often much closer to $r$ than $x_n$ is. – André Nicolas Apr 04 '13 at 03:18
-
4One thing to note is that it doesn't always work. – Thomas Andrews Apr 04 '13 at 04:04
-
2There are two Newton's method, one for root finding and one for optimisation. While the two are closely related, the community can offer better help if you could clarify which Newton's method you are talking about. – user1551 Apr 04 '13 at 04:37
-
2@user1551, ...and the "optimization" version is more or less applying the "root finding" version to the derivative of your function, of course. – J. M. ain't a mathematician Apr 04 '13 at 05:21
-
2@J.M. Sure, but seeing that all you guys here were only talking about the "root finding" version, if the OP was asking about the "optimisation" version, I thought he might be puzzled. :-D – user1551 Apr 04 '13 at 05:36
-
@ThomasAndrews: I think this is an important point, see my answer below: http://math.stackexchange.com/a/2093447/346 – vonjd Jan 11 '17 at 15:15
4 Answers
The method is easiest to justify in one dimension. Say that I have some complicated function $f(x)$ whose root I want to find:
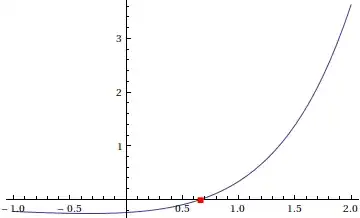
"I don't know how to find its root; it's complicated!" Thus, we use a general idea that has always been used in the design of numerical methods:
Replace a complicated function with a simple approximation.
One of the simplest functions one can deal with is a linear function:
$$f(x)=mx+b$$
In particular, if you want the root of a linear function, it's quite easily figured:
$$x=-\frac{b}{m}$$
Now, it is well-known (or at least, ought to be) that the tangent line of a function is the "best" linear approximation of a function in the vicinity of its point of tangency:

The first idea of the Newton-Raphson method is that, since it is easy to find the root of a linear function, we pretend that our complicated function is a line, and then find the root of a line, with the hope that the line's crossing is an excellent approximation to the root we actually need.
Mathematically, if we have the tangent line of $f(x)$ at $x=a$, where $a$ is the "starting point":
$$f(x)\approx f(a)+f^\prime(a)(x-a)=0$$
If we want $x$, then
$$x=a-\frac{f(a)}{f^\prime(a)}$$
Let's call this $x_1$.
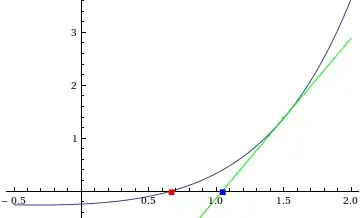
As you can see, the blue point corresponding to the approximation is a bit far off, which brings us to the second idea of Newton-Raphson: if at first you don't succeed, try again:
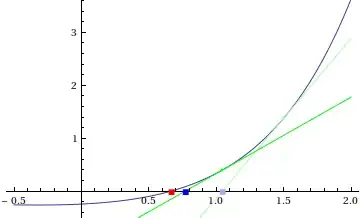
As you can see, the new blue point is much nearer to the red point. Mathematically, this corresponds to finding the root of the new tangent line at $x=x_1$:
$$x_2=x_1-\frac{f(x_1)}{f^\prime(x_1)}$$
We can keep playing this game (with $x_2, x_3, \dots x_n$), up until the point that we find a value where the quantity $\dfrac{f(x_n)}{f^\prime(x_n)}$ is "tiny". We then say that we have converged to an approximation of the root. That is the essence of Newton-Raphson.
As an aside, the previous discussion should tip you on what might happen if the tangent line is nearly horizontal, which is one of the disastrous things that can happen while applying the method.
- 76,540
-
1
-
1A minor quibble to a great answer: in the third graph I would mark the point of tangency with blue to show the function value at the first approximation, then make the new putative root some other color. – Ross Millikan May 19 '13 at 04:41
-
@Ross, I'll see if I can redo the images later; I lost the code for generating them... anyway, the idea I had with the coloring is to denote the previous approximation with a lighter hue than the current one, as if leaving a "shadow". – J. M. ain't a mathematician May 19 '13 at 04:45
-
This animation from the Wikipedia page for Newton's Method might be useful:
- 186,215
Most root finding methods work by replacing the function, which is only known at a few points, with a plausible model, and finding the root of the model.
For instance, the chord and regula falsi methods work from two known points and hypothetise a linear behavior in between. Newton uses a single known point and the direction of the tangent, and also hypothesizes a linear behavior. Brent uses three points and a parabolic interpolation.
In all cases, the reason why it works is simple: because the new estimate is closer to the root.
For this property to hold, the functions must satisfy certain criteria, which are established in the frame of calculus, and essentially mean that the function can be well fitted by the model. In particular, when the function has Taylor develomments, it locally behaves like a polynomial of some degree.
Just to add to @J.M.isn'tamathematician's excellent answer to further the intuition by showing what can go wrong: He correctly states that
the second idea of Newton-Raphson: if at first you don't succeed, try again
and
As an aside, the previous discussion should tip you on what might happen if the tangent line is nearly horizontal, which is one of the disastrous things that can happen while applying the method.
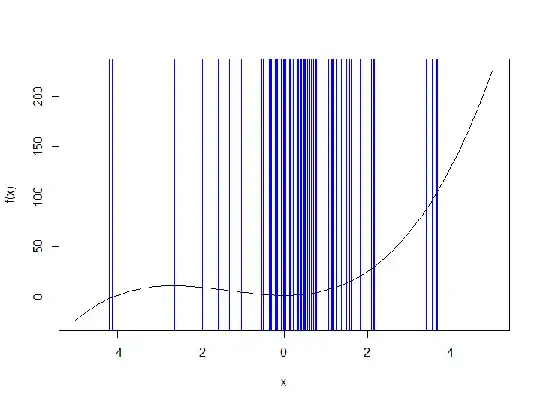
Now take $f(x) = x^3 + 4x^2 + 2$ as an example. The problem with this function is that it has a local minimum at $x = 0$. So chances are that Newton's method doesn't converge well and kind of gets stuck at this point (start value $x_0 = -0.2$):
It needs nearly one hundred steps to converge to the correct root:
[1] 1.25405405 0.55828951 -0.07502307 3.39162274 1.97982246 1.05803843 0.40994332 -0.31450666 0.75093645 0.14320131 -1.58400496
[12] -0.01701181 14.78153626 9.47525411 5.96420795 3.65606250 2.15153922 1.17158629 0.49714344 -0.16226289 1.56115458 0.77564951
[23] 0.16726898 -1.32110219 -0.06933876 3.66737868 2.15888881 1.17642792 0.50077832 -0.15671012 1.61818117 0.81479282 0.20416095
[34] -1.03294088 -0.01257056 19.97565197 12.92352671 8.24395239 5.15273877 3.12573832 1.80717017 0.94279300 0.31653240 -0.54214209
[45] 0.33079361 -0.50087321 0.38342862 -0.37029938 0.60879939 -0.01106036 22.69186757 14.72904585 9.44044843 5.94124669 3.64103655
[56] 2.14178046 1.16515554 0.49230607 -0.16973436 1.49006847 0.72642443 0.11865987 -1.95693378 0.40083226 -0.33305704 0.69914624
[67] 0.09047483 -2.62679347 33.89326353 22.18294416 14.39066991 9.21610201 5.79327581 3.54423074 2.07891422 1.12366889 0.46082599
[78] -0.22083802 1.12717058 0.46350213 -0.21631397 1.15277927 0.48296531 -0.18443552 1.36626938 0.63928788 0.02480862 -9.97181560
[89] -7.26371299 -5.56469935 -4.60454535 -4.20044316 -4.12094225 -4.11794646 -4.11794227 -4.11794227 -4.11794227
This shows that the second idea of Newton's method is only a heuristic which could fail in some cases.
- 9,040