Why does taking the tangent line improve the approximation in Newton's method?

Question

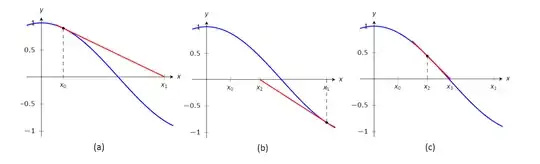
I have gained a comprehension of the operational process through the discussion located at Why does Newton's method work?. Nevertheless, there is one aspect that remains unclear to me.

To initiate, we choose a pair of values, $(x_0, f(x_0))$, where $x_0$ is in proximity to the true root of $f(x)$ that I am seeking. Subsequently, we determine the linearization of $f(x)$ at this point, denoted as $L_{x0}(x)$. In favorable conditions, I can identify the root of $L_{x0}(x)$, which I will refer to as $x_1$. It seems reasonable to anticipate that $x_1$ will provide a more accurate approximation to the true root of $f(x)$, which is the one I actually require.

However, I am uncertain about how creating a tangent line at the point $(x_1, f(x_1))$ will result in a more precise approximation, which we can designate as $x_2$, to the true root of $f(x)$ in comparison to $x_1$.

My explanation is that, for the same reason $x_1$ provided a superior approximation to the true root of $f(x)$ compared to $x_0$, $x_2$ offers a better approximation than $x_1$. Nonetheless, I am still unsure about my own response and remain open to any clarifications or insights on this matter.

Answer 1

So, Basically the question which you intend an answer for, which I have understood from the conversations is that.

How $L_{x_1}(x)$ provides a better approximation in the same way as $L_{x_0}(x)$ is defined?

At first, You take a point $x_0$ which is proximal to $x^*$ a root of $f$. Now, define $I_0 : [x^*,x_0]$ interval with absolute value $|x_0 - x^*|$. By linearization of $f$ at point $x_1$ we get an interval with absolute value $|x_1 - x^*|$.

The answer to your question is just equivalent to proving that,

$$|x_0 - x^*| \ge |x_1 - x^*|$$

Now $x_1 = x_0 - (f(x_0)/f'(x_0))$ by $L_{x_1}(x)$, So the equality would then demand $f(x_0)/f'(x_0) = 0$ $\implies$ either $f(x_0) = 0$ or $|f'(x_0)| \to \infty$ is satisfied.

With the above argument, You can prove that the $abs(I_0) \ge abs(I_1) \ge abs(I_2) ...... \ge abs(I_i)$. Here, the $abs(I_i)$ is defined as absolute value of the interval, $i \in Z^+$. ($I_i : [x^*,x_i]$)

Answer 2

When we take the tangent line from the point $f(x_o)$ the point where the tangent line intersects the x-axis is closer to the actual root than the previous proximity root thus improving the approximation and if we do it again we get a more and more better approximation

Answer 3

The intuition is that when you solve $L_{x_0}(x) = 0$ and get $x_1$, you're computing the root of a linear approximation of $f(x)$ calculated around the point $x_0$. This function approximation $L_{x_0}(x)$ coincides with $f(x)$ at $x = x_0$ and gets worse as $x$ gets farther from $x_0$.

Now say you assume $x_1$ is closer to the actual root $x_*$ of $f(x)$ than $x_0$ is. Then, at the actual root $x_*$, $L_{x_1}(x)$ approximates $f(x)$ better than $L_{x_0}$ does.

The post you linked provides some good graphical examples for this intuition.

Answer 4

The linked Wikipedia page also gives the analytic argument, recapitulated here. Suppose the root is at $x_\ast$ and the original guess is at $x_0$. Make a Taylor expansion of $f$ around $x_0$: $$ f(x_\ast) = f(x_0) + f'(x_0)(x_\ast - x_0) + \frac{1}{2} f''(t) (x_\ast-x_0)^2 $$ where $t$ is some number between $x_0$ and $x_\ast$. Now $f(x_\ast) = 0$, so $$ x_0 -\frac{f(x_0)}{f'(x_0)} = x_\ast - \frac{f''(t)}{2f'(x_0)}(x_\ast - x_0)^2 $$ The left-hand side is $x_1$. So $$ x_\ast - x_1 = -\frac{f''(t)}{2f'(x_0)}(x_\ast - x_0)^2 $$

The fraction is a bit tricky, but if there's an upper bound $C$ for it, you get that $|x_1 - x_\ast| \leq C |x_0 - x_\ast|^2$. So it's even better than a contraction mapping. Basically the number of decimal points of accuracy double each time.