Why does multiplying by the inverse of the Jacobian matrix generalize the Newton-Raphson method to n dimensions?

Question

I don't fully understand how multiplying by the inverse of the Jacobian matrix generalizes the Newton-Raphson method to $n$ dimensions.

In other words, I don't understand how this:

$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$

is equivalent to this in 2 dimensions:

$\begin{bmatrix} x_{n+1} \\y_{n+1} \end{bmatrix} = \begin{bmatrix} x_n \\y_n \end{bmatrix} - \begin{bmatrix} \frac{\partial f_1}{\partial x} & \frac{\partial f_1}{\partial y} \\ \frac{\partial f_2}{\partial x} & \frac{\partial f_2}{\partial y} \end{bmatrix}^{-1} \begin{bmatrix} f_1(x_n, y_n) \\f_2(x_n, y_n) \end{bmatrix}$

I guess since we multiply $\begin{bmatrix} f_1(x_n, y_n) \\f_2(x_n, y_n) \end{bmatrix}$ by the inverse of the Jacobian matrix, it's a bit like we divide it by its derivative but it doesn't sound that obvious to me mathematically.

Answer 1

Imagine space as a regular grid of boxes. You can visualize a nonlinear mapping, $f$, as a wavy distortion of those boxes, like in the following image: Finding a zero of $f$ means finding a point in the domain that gets mapped to $0$ in the range.

Locally, a smooth map may be approximated as a mapping that takes boxes to parallelograms (or parallelopipeds in higher dimensions), shown in orange in the following image:

This local approximation is the first order Taylor expansion, $$f(x,y) \approx f(x_0, y_0) + J(x_0, y_0) \left(\begin{bmatrix}x \\ y\end{bmatrix} - \begin{bmatrix}x_0 \\ y_0\end{bmatrix}\right),$$ where $J$ is the Jacobian matrix.

The idea of Newton's method is to replace wavy the nonlinear mapping $f$ with this local linearization:

Now finding the zero simply means solving the linear system $$\begin{bmatrix}0 \\ 0\end{bmatrix} = f(x_0, y_0) + J(x_0, y_0) \left(\begin{bmatrix}x \\ y\end{bmatrix} - \begin{bmatrix}x_0 \\ y_0\end{bmatrix}\right),$$ for $(x,y)$, and this is where the inverse of the Jacobian comes in.

Of course, because we made this approximation the solution we find will not be exact. However, it will get us closer to the true solution. At the new point we can linearize again, and repeat until convergence.

The nice thing is that the closer we get to the true solution, the smaller our steps are, and so the more accurate the linear approximation becomes. This is what causes Newton's method to converge very fast.

Answer 2

The mathematical justification for the formula is very simple. Use the linear Taylor expansion of the function $f(x_1, x_2)$ at the point $(x_1, x_2)$, you get

$ f(x_2 , y_2) = f(x_1, y_1) + J(x_1, y_1) ( x_2 - x_1, y_2 - y_1) $

Since we want $f(x_2, y_2)$ to be the zero vector, then

$ (x_2 - x_1, y_2 - y_1) = (\Delta x, \Delta y) = - J^{-1}(x_1, y_1) f(x_1, y_1) $

Answer 3

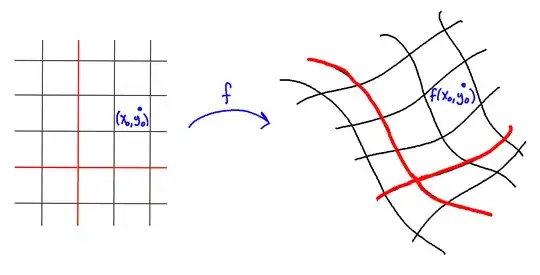
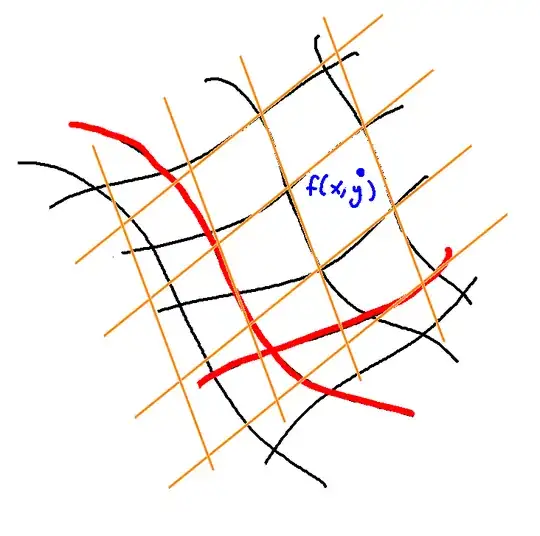
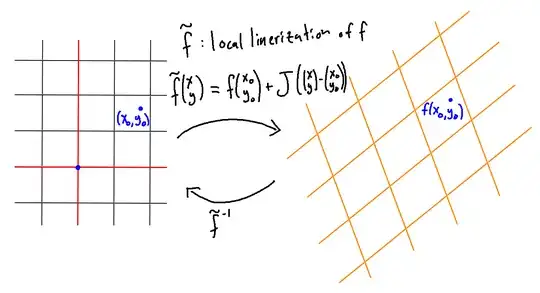
Ok I think I get it.

The Taylor formula is :

$f(x_{i+1}) = f(x_i) + f'(x_i)(x_{i+1} - x_i)$

So, if we're looking for a zero we can put :

$0 = f(x_i) + f'(x_i)(x_{i+1} - x_i)$

$0 = \frac{f(x_i)}{f'(x_i)} + x_{i+1} - x_i$

$x_{i+1} = x_i - \frac{f(x_i)}{f'(x_i)}$

And at the end, we get the Newton-Raphson formula.

If we do the same in 2 dimensions :

$\begin{bmatrix} f_1(x_{i+1}) \\ f_2(y_{i+1}) \end{bmatrix} = \begin{bmatrix} f_1(x_i) \\ f_2(y_i) \end{bmatrix} + \begin{bmatrix} \frac{\partial f_1}{\partial x} \frac{\partial f_1}{\partial y} \\ \frac{\partial f_2}{\partial x} \frac{\partial f_2}{\partial y}\end{bmatrix} \begin{bmatrix} x_{i+1} - x_i \\ y_{i+1} - y_i \end{bmatrix}$

which is equivalent to :

$F(x_{i+1}) = F(x_i) + J_F(x_i)(x_{i+1} - x_i)$

and if we develop we get this :

$\begin{bmatrix} f_1(x_{i+1}) \\ f_2(y_{i+1}) \end{bmatrix} = \begin{bmatrix} f_1(x_i) \\ f_2(y_i) \end{bmatrix} + \begin{bmatrix} \frac{\partial f_1}{\partial x}(x_{i+1} - x_i) + \frac{\partial f_1}{\partial y}(y_{i+1} - y_i) \\ \frac{\partial f_2}{\partial x}(x_{i+1} - x_i) + \frac{\partial f_2}{\partial y}(y_{i+1} - y_i) \end{bmatrix}$

$\begin{bmatrix} f_1(x_{i+1}) \\ f_2(y_{i+1}) \end{bmatrix} = \begin{bmatrix} f_1(x_i) + \frac{\partial f_1}{\partial x}(x_{i+1} - x_i) + \frac{\partial f_1}{\partial y}(y_{i+1} - y_i) \\ f_2(y_i) + \frac{\partial f_2}{\partial x}(x_{i+1} - x_i) + \frac{\partial f_2}{\partial y}(y_{i+1} - y_i) \end{bmatrix}$

We can see the Taylor formula again in 2 dimensions here. So if we want to get the Newton-Raphson formula, we just have to put this :

$F(x_{i+1}) = F(x_i) + J_F(x_i)(x_{i+1} - x_i)$

$0 = F(x_i) + J_F(x_i)(x_{i+1} - x_i)$

$0 = J_F^{-1}(x_i)F(x_i) + x_{i+1} - x_i$

$x_{i+1} = x_i - J_F^{-1}(x_i)F(x_i)$

and finally we get this mysterious formula.

(tbh I'm not super sure of my demonstration but I think it's a bit clearer for me now even so)