How close are the closests cells of the same color in a periodically colored grid?

Question

In a square grid, if we have a coloring of the form $c(x, y) = (x + ny) \bmod m$, what is the minimum (positive!) taxicab distance (i.e. sum of absolute value fo coordinates) between different cells of the same color?

(In this example I colored all values except for 0 the same color. We are interested in the distance between yellow cells.)

This is the same as minimizing the following function,

$$d(m, n) = |mk + n\ell| + |\ell|$$

for fixed $0 \leq m < n$, and $k, \ell$ are integers that can be chosen freely (not both 0).

Ideally, I would like a formula for the minimum value of $d$ in terms of $m$ and $n$.

For the example shown above, $m = 7, n = 3$, and we find the minimum of $d$ to be $3$ (with $k = -1$ and $\ell = 2$).

---

It looks like this should be very easy but I find it tricky in the general case.

Background: I came across this question: Minimum colors needed to color Z2 with connected subsets restriction, where a specific instance of this problem is used in the answer. This is also related to another question I asked: What is the minimum distance between vertices on an integer grid with the form $(m(m+2), 0)p + (m, 1)q$? (Although in that question the Euclidean distance rather than the taxicab distance is being minimized.)

---

Update: I wrote a program to calculate the value of $d(m, n)$. There are obviously patterns, although I have not worked out exactly what.

Here is the same data arranged in a triangle; obviously factors play a role.

One interesting observation: the maximum value in each row (for fixed $m$), is roughly $\sqrt{2m}$, and in fact exactly $\sqrt{2m}$ for $m = 2, 8, 18, 32, ...$ (whenever $m$ is double a perfect square).

Answer 1

There's a continuous variant of this problem that tells you pretty well why the patterns you see exist:

First, let $|\cdot |:\mathbb R \rightarrow [0,1/2]$ be the function that takes a real number to the distance from it to the closest integer. Let $m>0$ be a real number. Define a function $$f_m(x)=\min_{b\in\mathbb N}m|bx|+b.$$

In the main question, we are trying to find a non-trivial pair $a,b\in\mathbb Z$ minimizing $|a|+|b|$ such that $a+nb\equiv 0\pmod{m}$. If we divide through by $m$ we get $\frac{a}m + b\cdot \frac{n}m\equiv 0 \pmod{1}$. Note that, for any $b$, the size of the smallest $a$ possible to make this happen is $m\cdot |b\cdot \frac{n}m|$. As a result, we find that the closest point is exactly $f_m(n/m)$ away in the taxicab metric.

So, what is this function $f_k$ like? Well, you can write it as a minimum of other functions; Let $g_{m,a,b}(x)=m|bx-a|+b$ for $a,b\in\mathbb N$. This is just a "cone" of slope $mb$ with vertex at $\left(\frac{a}b,b\right)$. Then, we can express $$f_m=\min_{a,b}g_{m,a,b}$$ which basically tells us that, if we increase $m$ to be rather large, the only points with small distances will be those that are very close to $\frac{a}b$ for some small enough $b$. This is where the "stripes" in your diagram come from.

Here's an animation of the function $f_m$ over the interval $[0,1]$ for $m$ increasing from $1$ to $20$. Notice how, as the parameter increases, the function sweeps upwards and "catches" on the node points

Each of these "cones" where the function catches is a brief window of small values that persists whenever the ratio of that value to $m$ is there - and note that this does transfer to the set of evaluations only at multiples of $1/m$ since $g_{m,a,b}$ has slope $\pm mb$ everywhere, so has to be within $\frac{b}2$ of the minimum possible value for some multiple of $1/m$.

One can use Dirichlet's approximation theorem to show that the maximum of $f_m$ grows on the order of $\sqrt{m}$, as you observe; in particular, for every $x$, there must be some some pair of integers $a,b$ with $1 \leq b \leq \sqrt{m}$ so that $|bx-a| < \frac{1}{\sqrt{m}}$ - equivalently so that $g_{m,a,b}(x) \leq b + \sqrt{m} \leq 2\sqrt{m}.$ Thus $f_m(x) \leq 2\sqrt{m}$ everywhere. For a lower bound, one can note that $\frac{1}{2\sqrt{m}}$ is closer to $0$ than to any fraction with denominator at most $\sqrt{m}$, so $f_m\left(\frac{1}{2\sqrt{m}}\right) = \frac{\sqrt{m}}2$; if you're a little more careful, you can improve the lower bound fairly easily, although I'm not sure how to improve the upper bound.

Similar reasoning also gives a good hint at what you do if you want to compute $f_m(x)$, you only need to look at pairs $(a,b)$ where $|bx-a|$ is smaller than it is for any pair $(a',b')$ with smaller $b$; these are called best rational approximations of the second kind and are precisely the convergents $a/b$ of the continued fraction for $x$. Thus, to compute the value really quickly, you just compute $g_{m,a,b}(x)$ at convergents $a/b$ of $x$ until the smallest evaluation of this quantity is less than the denominator of the convergent you have reached - this should happen really quickly since the denominators of a continued fraction grow at least as fast as the sequence of Fibonacci numbers and you can definitely stop by the time the denominators have reached $m/2$. This also tells you that, for a fixed $x$, the growth of $f_m(x)$ is controlled by how quickly the convergents to $x$ converge to $x$.

Answer 2

$$\color{brown}{\mathbf{Preliminary\ notes.}}$$

If $\underline{\gcd(m,n)=g\not=1}$ then $\min\limits_{k,l}\, d(gm_1,gn_1,k,l) = \underline{(d(m_1,n_1,k_1,l_1)-l_1)g + l_1)}.$

If $\underline{n=1}$ then $\min\limits_{k,l}\, d(m,n,k,l) = \underline{n+1}\ $ at $(k,l)=(k_0,l_0) = (0,\pm1).$

If $\underline{n=m-1}$ then $\min\limits_{k,l}\, d(m,n,k,l) = \underline{2}\ $ at $(k,l)=(k_0,l_0) = (-1,1).$

If $\underline{n\in[2,m-2]}$ then WLOG $$\gcd(m,n) = 1,\ l\ge 0,\ k<0,\ \gcd(k,l)=1,\tag1$$ $$D_{m,n}=\min\limits_{k,l}\ d(m,n,k,l) =\min\limits_{k,l}\,\max\left|(m,n\pm1)\cdot(k,l)\large\mathstrut\right|.\tag2$$

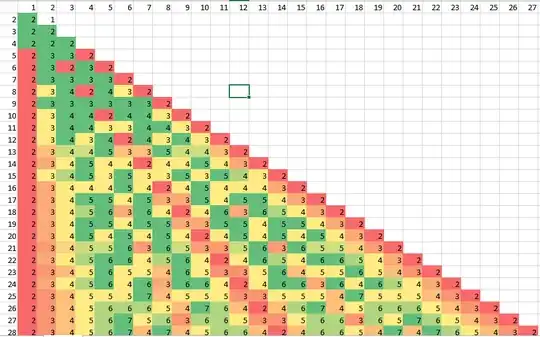
Formulas $(2)$ allows to calculate $D_{m,n}$ immediately, using the tables.

If $\underline{(m,n)=(7,3)}:$

$\left[\begin{matrix} \mathbf{(7,3)} & (-1,1) & (-1,2) & (-1,3) & (-2,3) & (-2,5)\\ (7,2) & 5 & 3 & 1 & 8 & 4 \\ (7,4) & 3 & 1 & 5 & 2 & 6 \\ \textbf{max} & 5 & \mathbf3 & 5 & 8 & 6 \\ \end{matrix}\right]$

If $\underline{(m,n)=(3,2)}:$

$\left[\begin{matrix} \mathbf{(3,2)} & (-1,0) & (-1,1) & (-1,2) & (-2,1) & (-2,3)\\ (3,1) & 3 & 2 & 1 & 5 & 3 \\ (3,3) & 3 & 0 & 3 & 3 & 0\\ \textbf{max} & 3 & \mathbf2 & 3 & 5 & 3\\ \end{matrix}\right]$

$$\color{brown}{\mathbf{Estimations.}}$$

Proposed task belongs to the discrete type of tasks, which exact solution in the common case can not be provided without option calculation algorithm. So universal solution of the given task in the closed form for all arbitrary unbounded values looks impossible.

However, for the bounded values of $n,$ exact solutions have closed form. Also, can be found solution for any given pair $(m,n).$

$\mathbf{Case\ k=-1.}$

Since $$m\in n\left[f(m,n),c(m,n)\large\mathstrut\right],$$ where $$f(m,n)=\left\lfloor\dfrac mn\right\rfloor,\quad c(m,n)=\left\lceil\dfrac mn \right\rceil.$$

This leads to the estimation

$$D_{m,n} \le \min\left\{F^{(1)}_{m,n},C^{(1)}_{m,n}\right\},$$ where $$F^{(1)}_{m,n} = d(m,n,-1,f(m,n)),\quad C^{(1)}_{m,n} = d(m,n,-1,c(m,n)),$$ or \begin{cases} F^{(1)}_{m,n} = \max\left\{m-(n-1)f(m,n),(n+1)f(m,n)-m\right\},\\ C^{(1)}_{m,n} = \max\left\{m-(n-1)c(m,n),(n+1)c(m,n)-m\right\}.\tag3 \end{cases}

In particular, the values $\ f(7,3) = 2 $ and $\ f(3,2)=1\ $ lead to the optimal solutions.

$\mathbf{Case\ k>1\ (first\ iteration).}$

If $n\!\!\not|\ m,$ then $$\dfrac mn - r_2\in\left[\cfrac 1{c(n,m-nr_2)},\cfrac 1{f(n,m-nr_2)}\right],$$ or $$m\in n\left[\dfrac{r_2c(n,m-nr_2)+1}{c(n,m-nr_2)},\dfrac{r_2f(n,m-nr_2)+1}{f(n,q_2)}\right]$$ where $$r_2=f(m,n).$$

This leads to the estimation

$$D_{m,n} \le \min\left\{F^{(2)}_{m,n},C^{(2)}_{m,n}\right\},$$ where $$F^{(2)}_{m,n} = d(m,n,-k^{(2)}_f,r_2k^{(2)}_f+1), \quad C^{(2)}_{m,n} = d(m,n,-k^{(2)}_c,r_2k^{(2)}_c+1),\tag4$$ $$k^{(2)}_f = \left\lfloor\dfrac n{m-nr_2}\right\rfloor, \quad k^{(2)}_c = \left\lceil\dfrac n{m-nr_2}\right\rceil.\tag5$$

$\mathbf{Case\ k>1\ (continued\ fraction\ estimations).}$

The alternative way is using of continued fraction decomposition in the form of $$\dfrac mn = [r^\,_{3,0};r^\,_{3,1},r^\,_{3,2},\dots,r^\,_{3,i}] =r^\,_{3,0} + \cfrac 1{r^\,_{3,1}+\cfrac 1{r^\,_{3,2}+\cfrac 1{\dots+\cfrac 1{r^\,_{3,i-1}+\cfrac1{r^\,_{3,i}}}}}}.$$

Similarly to the previous case, this leads to the estimations

$$D_{m,n} \le \min\left\{F^{(3)}_{m,n}(j),C^{(3)}_{m,n}(j)\right\},$$ where $$F^{(3)}_{m,n}(j) = d(m,n,-k^{(3)}_f(j),l^{(3)}_f(j)), \quad C^{(3)}_{m,n}(j) = d(m,n,-k^{(3)}_c(j),l^{(2)}_c(j)),\tag6$$ $$\dfrac{l^{(3)}_f(j)}{k^{(3)}_f(j)} = [r^\,_{3,0};r^\,_{3,1},r^\,_{3,2},\dots,r^\,_{3,j}], \quad \dfrac{l^{(3)}_c(j)}{k^{(3)}_c(j)} = [r^\,_{3,0};r^\,_{3,1},r^\,_{3,2},\dots,r^\,_{3,j}+1].\tag7$$

$$\color{brown}{\mathbf{Numeric\ modeling.}}$$

Let us consider the case of $(m,n) = (F_{i+1},F_i),$

where $F$ is Fibonacchi sequence.

$${\small\left[\begin{matrix} \mathbf{(5,3)} & (-1,1) & (-1,2) & (-2,3) & (-3,5) \\ (5,2) & 3 & 1 & 4 & 5 \\ (5,4) & 1 & 3 & 2 & 5 \\ \textbf{max} & \mathbf 3 & \mathbf3 & 4 & 8 \\ \end{matrix}\right]\ \left[\begin{matrix} \mathbf{(8,5)} & (-1,1) & (-1,2) & (-2,3) & (-3,5) \\ (8,4) & 4 & 0 & 4 & 4 \\ (8,6) & 2 & 4 & 2 & 6 \\ \textbf{max} & \mathbf 4 & \mathbf 4 & \mathbf 4 & 6 \\ \end{matrix}\right]} $$$$ {\small\left[\begin{matrix} \mathbf{(13,8)} & (-1,1) & (-1,2) & (-2,3) & (-3,5) \\ (13,7) & 6 & 1 & 5 & 4 \\ (13,9) & 4 & 5 & 1 & 6 \\ \textbf{max} & 6 & \mathbf5 & \mathbf5 & 8 \\ \end{matrix}\right]\ \left[\begin{matrix} \mathbf{(21,13)} & (-1,1) & (-1,2) & (-2,3) & (-3,5) \\ (21,12) & 9 & 3 & 6 & 3 \\ (21,14) & 7 & 7 & 0 & 7 \\ \textbf{max} & 9 & 7 & \mathbf 6 & 7 \\ \end{matrix}\right]} $$$$ {\small\left[\begin{matrix} \mathbf{(34,21)} & (-1,2) & (-2,3) & (-3,5) & (-5,8)\\ (34,20) & 6 & 8 & 2 & 10\\ (34,22) & 10 & 2 & 8 & 6\\ \textbf{max} & 10 & \mathbf 8 & \mathbf 8 & 10\\ \end{matrix}\right] \left[\begin{matrix} \mathbf{(55,34)} & (-1,2) & (-2,3) & (-3,5) & (-5,8)\\ (55,33) & 11 & 11 & 0 & 11\\ (55,35) & 20 & 5 & 10 & 5\\ \textbf{max} & 20 & 11 & \mathbf{10} & 11\\ \end{matrix}\right]}$$

Considered example illustrates that for $n>30$ simple models does not lead to exact solutions in the common case.

Taking in account unknown behavior of continued fraction approximations, existing of the common solution of the given task in the closed form looks impossible.

On the other hand, calculations of the optimal solution in the common case have logarithmic complexity by the value of m, because $2\log_5 m$ is a high bound of the length of the continued fraction sequence.

Answer 3

I do not know very well about these type of problem but I think this link may help https://books.google.co.in/books?id=OIpZxK8naikC&pg=PA104&lpg=PA104&dq=How+close+are+the+closest+cells+of+the+same+color+in+a+periodically+colored+grid?&source=bl&ots=u9o1Z7ZF8G&sig=ACfU3U1ekJGse9l9ZzTU_z3GGOsCQ2hMow&hl=en&sa=X&ved=2ahUKEwi-pMH9lMzmAhVayzgGHdGtBgMQ6AEwAXoECAwQAQ#v=onepage&q=How%20close%20are%20the%20closest%20cells%20of%20the%20same%20color%20in%20a%20periodically%20colored%20grid%3F&f=false.

If this does not satisfy you,you can comment below and I will remove my answer.