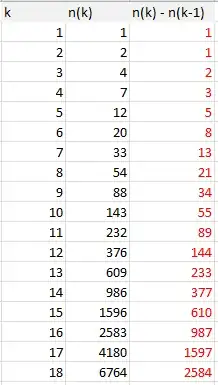
That is the same as asking about max number of runs (of consecutive 1's)
in a binary string of length $n=k-1$.
In this related post it is explained that the
Number of binary strings, with $s$ "$1$"'s and $m$ "$0$"'s in total, that have up to $r$ consecutive $1$s
is given by
$$
N_b (s,r,m + 1)\quad \left| {\;0 \leqslant \text{integers }s,m,r} \right.\quad
= \sum\limits_{\left( {0\, \leqslant } \right)\,\,k\,\,\left( { \leqslant \,\frac{s}{r+1}\, \leqslant \,m + 1} \right)} {
\left( { - 1} \right)^k \binom{m+1}{k}
\binom {s + m - k\left( {r + 1} \right) }{s - k\left( {r + 1} \right) }
}
$$
So, the cumulative number we are looking for is:
$$ \bbox[lightyellow] {
\eqalign{
& C(n,r) = \sum\limits_{\left( {0\, \le } \right)\,\,m\,\,\left( { \le \,n} \right)} {
N_b (n - m,r,m + 1)} = \cr
& = \sum\limits_{\left( {0\, \le } \right)\,\,m\,\,\left( { \le \,n} \right)} {
\sum\limits_{\left( {0\, \le } \right)\,\,k\,\,\left( { \le \,{s \over {r + 1}}\, \le \,m + 1} \right)} {\left( { - 1} \right)^k \binom{m+1}{k}
\binom{
n - k\left( {r + 1} \right)}
{n - m - k\left( {r + 1} \right) } } } \cr}
} \tag{1}$$
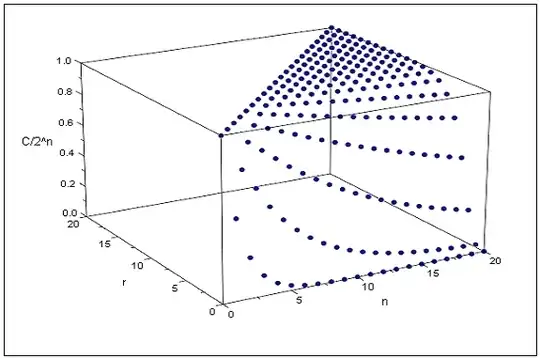
Of course it is $C(n,n)=2^n$.
It is also OEIS seq. A126198.
By splitting the first binomial in $m+1$ and applying
$$
\eqalign{
& {{z^{\,m} } \over {m!}}\left( {{d \over {dz}}} \right)^{\,m} \left( {1 + z} \right)^{\,n} = \sum\limits_{k\, \ge \,0} {\left( \matrix{
n \cr
k \cr} \right)\left( \matrix{
k \cr
m \cr} \right)\,\;z^{\,k} } = \cr
& = {{n^{\underline {\,m\,} } z^{\,m} } \over {m!}}\left( {1 + z} \right)^{\,n - m} = \left( \matrix{
n \cr
m \cr} \right)z^{\,m} \left( {1 + z} \right)^{\,n - m} \cr}
$$
we can express $C(n,r)$ also as
$$ \bbox[lightyellow] {
\eqalign{
& C(n,r) = \sum\limits_{0\, \le \,m\, \le \,n} {N_m (n,r,m)} \quad \left| {\;0 \le {\rm integers }m,n,r} \right.\quad = \cr
& = \sum\limits_{\left( {0\, \le } \right)\,\,k\,\,\left( { \le \,{n \over {r + 2}} \le \,{n \over {r + 1}}} \right)} {\left( { - 1} \right)^k \left( \matrix{
n - k\left( {r + 1} \right) \cr
n - k\left( {r + 2} \right) \cr} \right)2^{\,n - k\left( {r + 2} \right)} } + 2\sum\limits_{\left( {0\, \le } \right)\,\,k\,\,\left( {{{n + 1} \over {r + 2}} \le \,{n \over {r + 1}}} \right)} {\left( { - 1} \right)^k
\left( \matrix{ n - k\left( {r + 1} \right) \cr
n + 1 - k\left( {r + 2} \right) \cr} \right)2^{\,n - k\left( {r + 2} \right)} } = \cr
& = \sum\limits_{\left( {0\, \le } \right)\,\,k\,\,\left( { \le \,{{n + 1} \over {r + 2}} \le \,{n \over {r + 1}}} \right)} {\left( { - 1} \right)^k \left( {\left( \matrix{
n + 1 - k\left( {r + 1} \right) \cr
n + 1 - k\left( {r + 2} \right) \cr} \right) + \left( \matrix{
n - k\left( {r + 1} \right) \cr
n + 1 - k\left( {r + 2} \right) \cr} \right)} \right)2^{\,n - k\left( {r + 2} \right)} } \cr}
} \tag{2}$$
Using the o.g.f. for $Nb$ provided in the post above, it is possible to provide
quite a neat o.g.f. for $C(n,r)$ as
$$ \bbox[lightyellow] {
\eqalign{
& F(z,r) = \sum\limits_{0\, \le \,n} {C(n,r)z^{\,n} } = \cr
& = \sum\limits_{0\, \le \,n} {\sum\limits_{\left( {0\, \le } \right)\,\,m\,\,\left( { \le \,n} \right)} {z^{\,m} N_b (n - m,r,m + 1)z^{\,n - m} } } = \cr
& = \sum\limits_{0\, \le \,\,m} {z^{\,m} \left( {{{1 - z^{\,r + 1} } \over {1 - z}}} \right)^{m + 1} } = \left( {{{1 - z^{\,r + 1} } \over {1 - z}}} \right){1 \over {1 - z{{1 - z^{\,r + 1} } \over {1 - z}}}} = \cr
& = {{1 - z^{\,r + 1} } \over {1 - 2z + z^{\,r + 2} }} \cr}
} \tag{3}$$
From the above it comes that $C(n,r)$ is just a shifted version of the Higher -order Fibonacci Numbers, i.e.
$$
C(n,r) = F_{\,n + r + 1}^{\,\left( {r + 1} \right)}
$$
with the definition given therein.
In this interesting paper "A Simplified Binet Formula for k-Generalized Fibonacci Numbers" - G.P.B. Dresden, Z. Du
we learn that also the $(r+1)$-nacci numbers can be expressed by formulas similar to that of Binet, which leads to
$$ \bbox[lightyellow] {
\eqalign{
& C(n,r) = \sum\limits_{k = 0}^r {{{\alpha _{\,k} - 1} \over {2 + \left( {r + 2} \right)\left( {\alpha _{\,k} - 2} \right)}}\alpha _{\,k} ^{\,n + 1} }
\quad \left| \matrix{ \;1 \le r \hfill \cr
\;0 \le n \hfill \cr} \right. \cr
& \alpha _{\,0} , \cdots ,\alpha _{\,r} \;{\rm roots}\,{\rm of}\,x^{\,r + 1} - \left( {1 + x + \cdots + x^{\,r} } \right) \cr}
} \tag{4}$$
In that paper it is also shown that the polynomial $x^{\,r + 1} - \left( {1 + x + \cdots + x^{\,r} } \right)$ has only one root (call it $\alpha$) outside
of the unit circle, and which is real and
$$
2 - {1 \over {r + 1}} < \alpha < 2
$$
Therefore, asymptotically for large $n$ , we get
$$ \bbox[lightyellow] {
C(n,r) \approx {{\alpha - 1} \over {2 + \left( {r + 2} \right)\left( {\alpha - 2} \right)}}\alpha ^{\,n + 1} \quad \left| \matrix{
\;1 \le r \hfill \cr
\;n \to \infty \hfill \cr} \right.
} \tag{5}$$