3

Consider polynomials of the form: $$x^r-(1-x)^k,$$

for $r,k\ge2.$

$x\in(0,1).$

When $r=k$ the polynomial seems to be reducible, except at $r=k=2.$

Do the irreducible and reducible polynomials form a pattern when plotted?

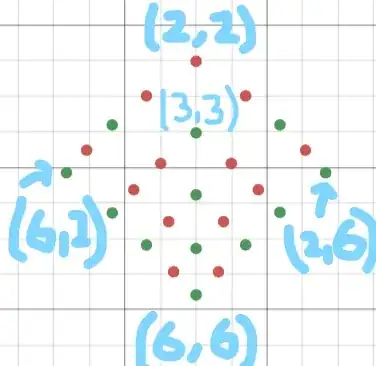
To try to visualise what was going on, I made a lattice of all the points representing reducible and irreducible polynomials of this form:

$$ x^r=(1-x)^k. $$

I plotted each solution $x$ at a certain height $h$ in such a way that the solutions formed a grid.

For example, all points greater than $2$ for $r=k,$ I colored green, because they are reducible, and plotted an $x$ value of $1/2$ and at different heights $h.$

Here's what it looks like for $r,k=\{2,3,4,5,6\}.$ Red=Irreducible, Green=Reducible.

enter image description here

J. Zimmerman
  • 842
  • I see a symmetry, but that is just because $x^r-(1-x)^k$ is irreducible iff $x^r-(1-x)^k$ (which is just application of $f(x)$ is irreducible iff $f(-x+1)$). Do you mean some other pattern? – Sil Mar 20 '19 at 22:50
  • @Sil I was also wondering if I could draw a line that goes through only red dots – J. Zimmerman Mar 20 '19 at 22:55

1 Answers1

2

Do the irreducible and reducible polynomials form a pattern when plotted?

Depends what you consider a pattern, but here are few quick observations. Let $f_{r,k}(x)=x^r-(1-x)^k$, then:

  • The graph is vertically symmetrical. This follows simply from fact that if $f(x)$ is irreducible, then $f(-x)$ is irreducible, as well as $f(x+1)$. In this case both together can be used to see $f(1-x)$ is irreducible iff $f(x)$ is irreducible, which applied to $f_{r,k}(x)=f_{k,r}(-x+1)$ gives you the vertical symmetry.

  • Middle vertical line is all consisting of green dots except for $(r,k)=2$. This is because for $r=k$ we have $f_{r,r}(x)=x^r-(1-x)^r$ is always multiple of $(2x-1)$ hence reducible. To see this (I'm sure there are easier ways), consider for example \begin{align*} f_{r,r}(x)&=x^r-(1-x)^r\\ &=(2x-1+(1-x))^r-(1-x)^r\\ &=\sum \binom{r}{i}(2x-1)^i (1-x)^{r-i}-(1-x)^r. \end{align*} All of the terms in the sum are multiples of $2x-1$ except for one with $i=0$, and so for some polynomial $P(x)$ we have \begin{align*} f_{r,r}(x)&=P(x)(2x-1)+(1-x)^r-(1-x)^r=P(x)(2x-1). \end{align*}

  • There is a vertical line going through just red dots. There is a family of polynomials $f_{r+1,r}(x)$ which seem to be irreducible (as well as they symmetrical counterpart $f_{r,r+1}(x)$). I could not find a proof suitable for all $r$'s, but I've checked for $r\leq 1000$ and they are all irreducible. Maybe someone will find a proof, but notice that such sequences of irreducible polynomials are quite common, the real challenge is to prove it. For example consider:

Sil
  • 17,976