1

Consider three events $A,B,C$ such that $P(A)>0$, $P(B)>0$, and $P(C)>0$. The events are linked to each other through the constraints $P(A\cup B\cup C)=1$ and $P(A)=P(\overline{B})$.

We suppose $P(A)>P(B)$, strictly. Therefore, we expect the event $A$ to occur before the event $B$, which is more unlikely.

However, if we require $P(A)=P(\overline{B})$, we are asking that the time we need to wait for getting a success of $\overline{B}$ (i.e. to not observe the occurrence of the event $B$) is the same we expect to wait to see a success of $A$.

But this means that the event $B$ must have been already occurred, and this is in contradiction with the fact that $P(A)>P(B)$.

I am probably doing some conceptual mistake, but I cannot see it. Moreover, what is the role of the event $C$ in all of this, since $P(A\cup B\cup C)=1$?

This post refers to this one A problem of conditional probability

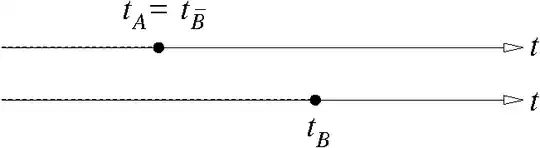
enter image description here

In this picture (sorry for raw format) $t_A,t_B$ represent the time we expected to wait to see the event $A$ and the event $B$, respectively (the dashed lines represent the time in which we expect the events not to happen). How does the constrain $P(A)=P(\overline{B})$ look like in this scheme?

Thanks for your suggestions!

  • What do you mean with "we expect the event $A$ to occur before the event $B$"? Is there any awareness of time built in the probabilistic model that you are studying? – drhab Jun 21 '18 at 11:19
  • Yes, drhab. We can imagine $A,B,C$ as events occurring in time, or trials, as for instance "to get a marble of color $A$ from an urn containing three types of marbles", while performing $t$ trials. –  Jun 21 '18 at 11:22
  • But can you say that event $A$ occurs before event $B$ purely on base of $P(A)>P(B)$?? – drhab Jun 21 '18 at 11:53
  • Of course not, I just can say that is more likely that the event $A$ occurs before the event $B$. Imagine that in your urn you have 1000000 marbles of type $A$, 10 marbles of type $B$ and 1 marble of type $C$. If you begin your trials, which color you expect to get first? –  Jun 21 '18 at 12:11
  • To build in time in your model you should refix your model and state events like $A_i,B_i,C_i$ for $i=1,2,\dots$ (or $A_t,B_t,C_t$ for $t\in[0,\infty)$). There $A_i$ is the event a marble of type $A$ was chosen at time $i$. – drhab Jun 21 '18 at 12:27

2 Answers2

1

In any kind of settings where the temporal language that you are using makes sense, what you forget here (when you say "this means that the event B must have been already occurred") is that $\bar B$ could occur first, before anything else happens. Especially before $B$ happens.

Therefore there is no contradiction.

Edit: an example to clarify things. Say you roll a die with $100$ equiprobable faces again and again, and "time" corresponds to the increasing number of tries.

Say $A=$ "get a number larger than $1$" and $B=$ "get $100$", and $C$ is whatever you like. Clearly $P(A)=P(\overline B)=\frac{99}{100}$ and $P(A\cup B\cup C)=1$.

As you roll the die (as time goes) you see that more likely than not the event $\overline B$ will occur immediately at the start of the experiment. It is wrong to think that to negate $B$ you first need to have $B$.

Arnaud Mortier
  • 27,742
  • Thanks for your answer, Arnaud! But I don't fully understand it. Can you expand your point a bit more? –  Jun 21 '18 at 10:59
  • 1
    When you say that you wait for $\bar B$ to happen, you seem to imply that $B$ has to happen before $\bar B$ can happen, and that is how you obtain a contradiction, isn't it? – Arnaud Mortier Jun 21 '18 at 11:18
  • Yes. And this is wrong? –  Jun 21 '18 at 11:26
  • I add a picture in the OP. Can you show me how the constraint $P(A)=P(\overline{B})$ should reflect on it? –  Jun 21 '18 at 11:30
  • @andrea.prunotto Yes it is wrong. I am not certain how you can imagine that it is true. I will add an example. – Arnaud Mortier Jun 21 '18 at 12:25
  • Thanks Arnaud. I am trying to figure this out in the above scheme, but I have troubles! –  Jun 21 '18 at 12:27
  • Thanks for your example, Arnaud! It is clear now. Don't you think there should be a way to visualize this idea in the context of the picture above? –  Jun 21 '18 at 13:02
  • @andrea.prunotto You're welcome! If you want to think in terms of pictures, you can imagine that the timeline that you drew is a target, and that you are throwing darts at this target. The event $A$ would then be "landing the dart on the right of the mark $t_A$". – Arnaud Mortier Jun 21 '18 at 13:17
  • True. And how to visualize, then, the constraint $P(A)=P(\overline{B})$? –  Jun 21 '18 at 13:23
  • 1
    @andrea.prunotto It's the fact that your two dots ($t_A$ and $t_B$) are symmetric with respect to the midpoint of the target. – Arnaud Mortier Jun 21 '18 at 13:24
  • Hmmm... Really? Can you explain me why? Sorry, I am not as clever as you : ) I guess you imply that there should be a "maximum time"? –  Jun 21 '18 at 13:30
  • 1
    @andrea.prunotto In the "target/darts" version, yes, the target is of finite length. The probability of hitting a certain area is the proportional size of that area compared to that of the whole target. – Arnaud Mortier Jun 21 '18 at 13:48
  • Sure. Got it! Thank you very much, Arnaud! In case, I invite you to have a look to my other post https://math.stackexchange.com/q/2826589/559615 It might interest you! Thanks again!!! –  Jun 21 '18 at 13:52
1

Your story is about a Venn diagram, and nothing more. Not about events happening sooner or later, or more often, etc. Just happening or not happening is the question. It could belong to the following setup:

Yesterday the cookie jar was full, and now half of the cookies are gone. There are three children who could have eaten from the cookies. Denote by $A$ the event that Alice has eaten some cookies, and similarly for $B$ and $C$.

The corresponding Venn diagram contains $7$ subsets with probability entries $x_k\geq 0$, whereby $\sum_{k=1}^7 x_k=1$. Furthermore there are two easily satisfiable linear conditions among the $x_k$. No big deal.

Christian Blatter
  • 232,144
  • Thanks for your answer, Christian, but I disagree. The event $A$ (and so on) can be, for instance, "to get, in $n$ independent trials, one element of kind $A$" from your jar, and therefore the whole problem can be studied in terms of expected number of trials to get the first success of the events in study, i.e. in terms of time. My problem is, in this context, how to interpret the supplementary constraint $P(A)=P(\overline{B})$. Please, tell me if you have any idea related to this problem (e.g. how to see this constraint in the picture above). Thanks again! –  Jun 21 '18 at 12:52