1

Consider three events $A,B,C$ such that $P(A)>0$, $P(B)>0$, and $P(C)>0$. The events are dependent to each other through the constraints $P(A\cup B\cup C) = 1$ and $P(A)=P(\overline{B})$. Under these conditions, I have to study the probability of the event $A\cap B\cap C$. By means of Bayes' theorem, I have obtained the following relation: $$ P(A\cap B\cap C)=\frac{P(A\cap B\cap C|B)P(A\cap B\cap C|A)}{P(A\cap B\cap C|B)+P(A\cap B\cap C|A)}. $$

In fact, being $I=A\cap B\cap C$, we have $P(I|A)P(A)=P(A|I)P(I)$ and $P(I|B)P(B)=P(B|I)P(I)$. Clearly, $P(A|I)=P(B|I)=1$. Therefore, applying the definition of opposite event $P(\overline{B})=1-P(B)$, and assuming $P(I|A)>0$, $P(I|B)>0$, we have $P(A)=\frac{P(I)}{P(I|A)}$ and $P(\overline{B})=1-\frac{P(I)}{P(I|B)}$. Equaling these two expressions (in which, however, I did not use the constraint $P(A\cup B\cup C)=1$) we obtain the above, highlighted relation.

On the other hand, by means of the principle of inclusion-exclusion, I have also found that $$ P(A\cap B\cap C)=P(A\cap B)+P(A\cap C)+P(B\cap C)-P(C). $$

In fact, $$P(A\cup B\cup C)=P(A)+P(B)+P(C)-P(A\cap B)-P(B\cap C)-P(A\cap C)+P(A\cap B\cap C),$$ and $$ P(A\cap B\cap C)=\underbrace{P(A\cup B\cup C)}_{=1}-P(A)-P(B)-P(C)+P(A\cap B)+P(B\cap C)+P(A\cap C). $$ If we substitute the other constraint $P(A)=P(\overline{B})$, or $1-P(B)-P(A)=0$, in this expression, we obtain the second highlighted relation.

My question is this:###

From the first relation, it seems that $P(A\cap B\cap C)$ depends only on the knowledge of the occurrence of $A$ and $B$, but the second one seems to assess an explicit dependence of $P(A\cap B\cap C)$ from $P(C)$. What's wrong here?

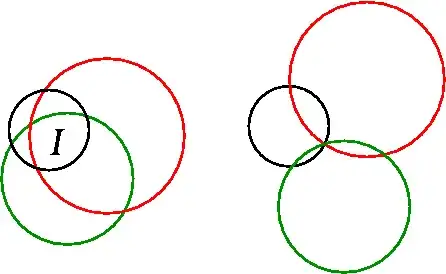
My suspect is illustrated in this picture, where the three events are depicted as sets of different colors:

Intersection is empty?

I wonder if the two constraints are moving the situation on the left to the one on the right, in which $P(I)=P(A\cap B\cap C)=0$. Somehow, it seems to me that the constraint I did not use to get the first relation (i.e. $P(A\cup B\cup C)=1$) requires $P(I)=0$ therein.

Community
  • 1
  • given that $P(A) = P(\bar{B})$ I think we can say that C is contained within A, by which I mean $C \subseteq A$. So $P(C) \leq P(A)$

    Therefore, $P(A \cap C) = P(C)$

     – Ben Crossley Jun 20 '18 at 21:42
  • 2
    No, @BenCrossley , we cannot say that. Counter example: Let the sample space be ${1,2,3,4}$ with $A={1,2}, B={1,3}, C={1,4}$. Then $\mathsf P(A\cap B\cap C)>0$, $P(A)=P(\overline B)$, and $P(A\cup B\cup C)=1$ but $C$ is not a subset of either from $A$ or $B$. – Graham Kemp Jun 21 '18 at 00:01
  • Thanks for your comments! I agree with Graham, Ben. I don't think one can conclude that $C$ is contained in $A$. @Graham: Thanks for pointing this out, but do you have any idea about the original question? –  Jun 21 '18 at 04:30
  • I explicit all the calculations that led me to the two relations. What worries me is that in the first one I did not use the constraint $P(A\cup B\cup C)=1$ and I had to assume $P(I)>0$. –  Jun 21 '18 at 04:55
  • 1
    Indeed the condition $P(A\cup B\cup C)=1$ is not needed to reach your first formula... which is a rather apparent tautology anyway: since $I\subseteq A$ and $I\subseteq B$, $$P(I\mid A)=\frac{P(I)}{P(A)}\qquad P(I\mid B)=\frac{P(I)}{P(B)}$$ Using this remark four times in the ratio on the RHS, one reaches the expression $$P(I)\frac{\frac1{P(B)}\frac1{P(A)}}{\frac1{P(B)}+\frac1{P(A)}}=P(I)\frac1{P(A)+P(B)}$$ hence the hypothesis $P(A)+P(B)=1$ is necessary and suffices to get LHS = RHS. – Did Jun 21 '18 at 05:34
  • 1
    This shows that, if $P(A)+P(B)=1$, then, for every $D\subseteq A\cap B$, $$P(D)=\frac{P(D\mid A)P(D\mid B)}{P(D\mid A)+P(D\mid B)}$$ – Did Jun 21 '18 at 05:40
  • Thanks Did, very clear! I see very well your point. However, in order to write the general formula (with $D$) you have to assume $P(D|A)>0$ and $P(D|B)>0$. But, then, what do you think about the conjecture $P(I)=0$? –  Jun 21 '18 at 06:07
  • Since $P(A) + P(B) = 1$, the first formula reduces to

    $P(A\cap B\cap C) = P(A\cap B\cap C)$

    which is in fact a is way to express the dependence of the RHS of C.

     – Boyku Jun 21 '18 at 09:20
  • Yes, @nbeginner. But in order to obtain the tautology you have to admit that $P(A\cap B\cap C)\neq 0$. My problem with this is illustrated in the picture, and it is still unanswered. Any idea? –  Jun 21 '18 at 09:29
  • @andrea.prunotto Actually the necessary condition is that $P(D\mid A)\ne0$ or $P(D\mid B)\ne0$ (not "and"). Regarding what happens when $P(A\cap B\cap C)=0$ in your question, the answer is much simpler: the proposed formula divides $0$ by $0$ hence it is not valid. Finally, I have no idea what your "conjecture" that $P(I)=0$ means, where it comes from and why you think you need it. (Unrelated: Please use @.) – Did Jun 23 '18 at 07:51

1 Answers1

0

The constraints on $C$ are too light to say anything. Basically anything could happen. You know that $$A\cap B\cap C\subseteq A \text{ (and $\subseteq B$, and $\subseteq C$)}$$ from which follows $$0\leq P(A\cap B\cap C)\leq \min(P(A),P(B),P(C))$$ and in fact $P(A\cap B\cap C)$ could be anything between $0$ and $\min(P(A),P(B),P(C)$).

Example where it is $0$: pick $B=\overline A$, in any situation where $0<P(A)<1$ (so that $P(B)>0$ as well). Then $P(A\cup B\cup C)=1$ and $C$ could literally be any event at all, the conditions would be met and $P(A\cap B\cap C)=0$ since $P(A\cap B)=0$.

Example where it is $P(B)$: Say you roll a die with $100$ equiprobable faces again and again, and say $A=$ "get a number larger than $1$" and $B=$ "get $100$". Clearly $P(A)=P(\overline B)=\frac{99}{100}$. Choose $C=B$. Then $A\cap B\cap C=B$.

You can cook up different examples by varying the overlap between $A$ and $B$.

Arnaud Mortier
  • 27,742