2

(I am not expert in English. I will write as well as I can.)

I ask this question because I want to solve

(What is minimum speed needed to jump over sphere object that has radius R and at distance d?)

But I think I have to this question before. This question is like that question but condition to find u minimum is less complex.

If I know how to solve this question, I may be able to solve that question.

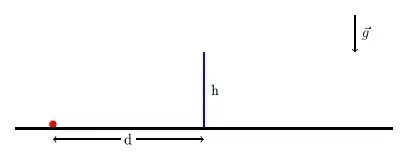
To understand this question easier, lets see this picture.

enter image description here

From this picture, what is minimum initial speed to throw red ball over this blue wall?

(assume red ball is very small and throw form h=0 and blue wall is very thin)

d and h can be any positive real number. g is a gravitational acceleration(approximately 9.80665 $m/s^2$).

This is a mathematical-physics question but mainly in maths.

I can do physics part but have problem in maths part.

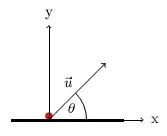
Physics Part : Let red ball in all pictures is at origin point and y is height

enter image description here

The relation between x and y for projectile motion is $y(x) = xtan\theta - \frac{gx^2}{2u^2cos^2\theta}$ , $0 < \theta < \frac{\pi}{2}$

Condition of the wall is $y(d) \geq h$ but for $u_{min}$, $y(d) = h$

$dtan\theta - \frac{gd^2}{2u^2cos^2\theta} = h$

$tan\theta - \frac{gd}{2u^2cos^2\theta} = \frac{h}{d}$

$\frac{gd}{2u^2cos^2\theta} = tan\theta - \frac{h}{d}$

$\frac{1}{u^2} = \frac{2cos^2\theta}{gd}( tan\theta - \frac{h}{d} )$

$u = \sqrt{ \frac{gd}{2cos^2\theta( tan\theta - \frac{h}{d} )} }$

At this point, I don't how to find $u_{min}(d,h)$ from this equation.

(If you give value of d and h (for example, d = 2m and h = 1m), it is possible to find $\theta$ that minimize u.)

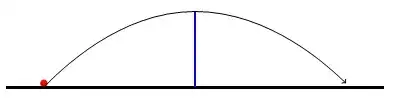
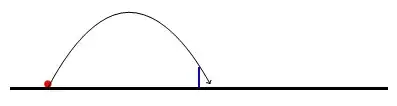
I know only that y(x) (parabola curve) for $u_{min}(d,h)$ look like.

Case : d $\leq$ ch (c is a constant. There is a ratio that if d > ch , y(x) won't have maximun point at the top of the wall.)

enter image description here

Case : d > c*h

enter image description here

Please help me.

Ted Shifrin
  • 125,228
Ro Theory
  • 815
  • at $u_{min}$ , $2\theta = -\tan^{-1}\frac{d}{h}$ $$\sin(2\theta) = \frac{d}{\sqrt{d^2+h^2}} , \cos(2\theta) = -\frac{h}{\sqrt{d^2+h^2}}$$ $$u = \sqrt{ \frac{gd}{2\cos^2\theta( \tan\theta - \frac{h}{d} )} }$$ $$ = \sqrt{ \frac{gd}{\sin(2\theta)-\frac{h}{d}(1+\cos(2\theta))} }$$ $$ = \sqrt{ \frac{gd}{ \frac{d}{\sqrt{d^2+h^2}}-\frac{h}{d}(1-\frac{h}{\sqrt{d^2+h^2}})} }$$ $$ = \sqrt{ \frac{gd}{ \frac{d+h}{\sqrt{d^2+h^2}}-\frac{h}{d} } }$$ – Ro Theory Apr 26 '18 at 17:10
  • Last line is false. It must be $$= \sqrt{\frac{gd}{ \frac{d}{\sqrt{d^2+h^2}} + \frac{h^2}{d\sqrt{d^2+h^2}} - \frac{h}{d} }}$$ $$= \sqrt{\frac{gd}{ \frac{d^2+h^2}{d\sqrt{d^2+h^2}} - \frac{h}{d} }}$$ $$= \sqrt{\frac{gd}{ \frac{\sqrt{d^2+h^2}-h}{d} }}$$ $$= \sqrt{g(\sqrt{d^2+h^2}+h)}$$ – Ro Theory Apr 27 '18 at 07:47

3 Answers3

2

Substituting $(d,h)$ into the standard projectile trajectory equation gives $$\begin{align}h&=d\tan\theta-\frac {gd^2}{2u^2\cos^2\theta}\\ u^2&=\frac {gd^2}{2\cos^2\theta(d\tan\theta-h)}\\ &=\frac {gd^2}{2(d\sin\theta\cos\theta-h\cos^2\theta)}\\ &=\frac {gd^2}{d\sin2\theta-h(1-\cos 2\theta)}\\ &=\frac {gd^2}{R(\frac dR\sin2\theta+\frac hR\cos 2\theta) -h} &&\scriptsize(R=\sqrt{d^2+h^2})\\ &=\frac {g(R^2-h^2)}{R(\sin2\theta\cos\alpha+\cos 2\theta\sin\alpha) -h} &&\scriptsize(\tan\alpha=h/d)\\ &=\frac {g(R^2-h^2)}{R(\underbrace{\sin(2\theta-\alpha))}_{<=1}-h}\\ {u^*}^2&=\frac {g(R^2-h^2)}{R-h} &&\scriptsize (u^*=\text{minimum launch velocity})\\\ &=g(R+h)\\ &=\color{red}{g(\sqrt{d^2+h^2}+h)} \end{align}$$ Note that launch velocity is at a minimum when $2\theta-\alpha=\frac\pi2$, i.e. when $\theta=\frac\pi 4+\frac\alpha 2$.

Hypergeometricx
  • 23,235
1

You've started just fine, but then lost the forest for the trees, I think. You want to maximize the function $$f(\theta) = \sin(2\theta)-\frac{2h}d \cos^2\theta.$$ ($f(\theta)$ gives a constant times the quantity $1/u^2$ needed to achieve height $h$ at horizontal distance $d$.)

Basic calculus tells you that this function has a unique critical point on $(0,\pi/2)$ and that it is the maximum point. That maximum occurs when $$\tan(2\theta) = -\frac dh.$$

Ted Shifrin
  • 125,228
  • Excuse me, I don't understand. I don't know how to get $f(\theta) = \sin(2\theta)-\frac{2h}d \cos^2\theta.$. – Ro Theory Apr 25 '18 at 20:19
  • Just go a step back when you solved for your equation for $u$. What's $1/u^2$? – Ted Shifrin Apr 25 '18 at 20:22
  • $$f(\theta) = \sin(2\theta)-\frac{2h}d \cos^2\theta = \sin(2\theta)-\frac{h}d (1+\cos2\theta)$$ $$f'(\theta) = 0 = 2\cos(2\theta)-\frac{h}{d} (0-2\sin(2\theta) $$ $$-\frac{h}{d}\sin(2\theta) = \cos(2\theta) $$ $$\tan(2\theta) = -\frac{d}{h} $$ But I don't get $\tan(2\theta) = -\frac{d}{2h} $ – Ro Theory Apr 26 '18 at 07:20
  • $(2\cos^2\theta)*( \tan\theta - \frac{h}{d} ) = \sin2\theta - \frac{2h}{d}\cos^2\theta$ – Ro Theory Apr 26 '18 at 13:08
  • You're absolutely correct. I mistyped, and have corrected my wrong $2$. – Ted Shifrin Apr 26 '18 at 14:30
  • Thank you very much. Could me solve ( https://math.stackexchange.com/questions/2745093/what-is-minimum-speed-needed-to-jump-over-sphere-object-that-has-radius-r-and-at ) This question seem much easier than that question and I think still unable to solve that question. – Ro Theory Apr 26 '18 at 15:43
  • If you're satisfied with my answer, please accept it so that this question will no longer appear unanswered. – Ted Shifrin Apr 26 '18 at 17:57
  • @RoTheory: I've written a rather detailed "answer" to your other question. You're going to need to implement it using a computer, nevertheless, as you get equations you certainly can't solve by hand. – Ted Shifrin Apr 26 '18 at 21:57
  • A nice geometric fact is that the direction in which you should throw the ball is the angle bisector of the vertical line through the starting position and the line through the starting position and the top of the wall. – David K Apr 26 '18 at 23:43
  • @DavidK Is there a way to see this a priori? – Ted Shifrin Apr 26 '18 at 23:44
  • @TedShifrin I got it by assuming the wall is at the maximum range on the line from the origin to the top of the wall, throwing at some fixed initial speed. If the speed were any greater you could overshoot the wall, so this is also the minimum speed for the given range. For a given speed there is a circle tangent to the line such that if you aim at any point on the circle the shot will fall directly below that point. To maximize range you aim at the farthest right point. This bisects the arc from $y$-axis to $y$-axis and therefore also bisects the angle I described. – David K Apr 26 '18 at 23:49
0

The last solutions is absolutely correct and complete, however, I would suggest a slightly different approach which would simplify the Math.

Instead of looking for a minimum of launch velocity $u$, one could solve for a maximum of the following (inverse) quantity: $C = g/u^2$,

$$C d^2= - h + h \cos (2 \theta) + d \sin(2 \theta)$$

$$C_{\max} d^2 = - h + \sqrt{h^2+d^2}$$

Sebastiano
  • 8,290
Andrii I
  • 1